OPERAZIONI CON GLI INSIEMI
INTERSEZIONE
L’intersezione di due insiemi A e B è l’insieme costituito dagli elementi che appartengono sia ad A che B.
Per esempio:
A={x/x lettera della parola gatto } B={x/x vocale della parola salto}
formeremo un terzo insieme C =A∩B={a,o,t } dove ∩ significa intersecato.
Vediamo altre esempi in rappresentazione tabulare
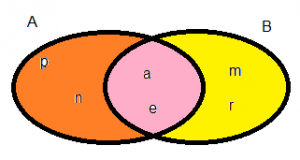
A={p,a,n,e} B={m,a,r,e } A∩B={a,e }
In rappresentazione mediante Eurelo-Venn
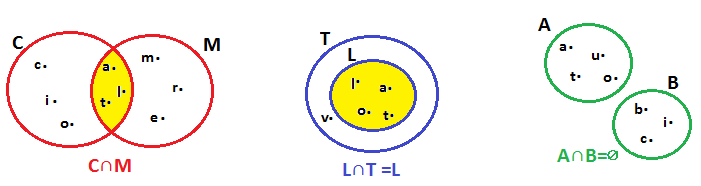
Se L = {x/x è una lettera della parola lato } T={x/x è una lettera della parola tavolo}
L’insieme L è sottoinsieme di T e si ha: L∩T ={l,a,t,o } = L quindi l’intersezione e sottoinsieme improprio di L, poichè coincide con L
Due insiemi si dicono DISGIUNTI se non hanno alcun elemento in comune A∩B=∅ cioè l’insieme vuoto.
Sono disgiunti l’insieme dei mammiferi e quello degli uccelli, perchè non esiste alcun uccello che sia mammifero.
Consideriamo tre esempi d’intersezione.
L’UNIONE
L’unione di due insieme A e B è l’insieme costituito da tutti gli elementi che appartengono sia ad A che a B, considerando una sola volta gli elementi comuni e si indica con A∪ B cioè A unito B.
Per esempio:
A={x/x lettera della parola gatto }; B={x\x lettera della parola salto };
In rappresentazione tabulare:
A={g,a,t,o }; B={s,a,l,t,o}; A∪B={g,a,t,o,s,l };
In rappresentazione grafica con Eurelo-Venn:
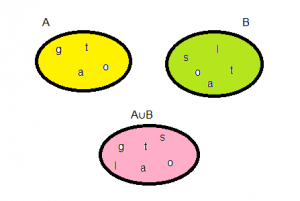
Considerando lo stesso esempio fatto per l’intersezione abbiamo:
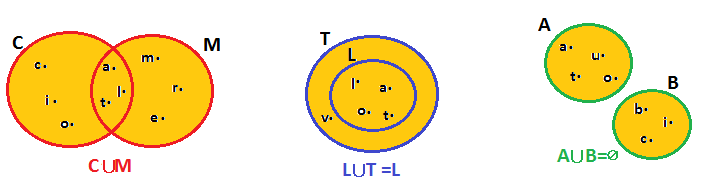
Vedi gli esercizi
Proprietà dell’intersezione
commutativa A∩B = B ∩ A
associativa (A∩B)∩C = A∩(B∩C)
distributiva rispetto all’unione A∩(B∪C) = (A∩B)∪ (A∩B)
Proprietà dell’unione
commutativa A∪B = B ∪ A
associativa (A∪B)∪C = A∪(B∪C)
distributiva rispetto al’intersezione A∪(B∩C) = (A∪B)∩ (A∪C)
LA DIFFERENZA
Si dice differenza di due insiemi A e B, considerati nell’ordine, l’insieme degli elementi di A che non appartengono a B.
Si scrive A – B e si legge “A – B”. In simboli A – B = {x|x ∈A e x ∉ B };
La differenza fra insiemi non è commutativa.
Esempio
1) A={5,6,7,8,9} B={1,2,3,5,6 } A-B= {7,8,9 }.
2) Consideriamo due insiemi di animali:
A={Agnello, oca, uccello, topo, ape}; B={topo, ape, lupo, rana};
A-B={agnello, oca, uccello}; quindi sono gli animali che appartengono ad A e non appartengono a B.
B-A={lupo, rana}.
L’INSIEME COMPLEMENTARE
Dato un insieme A e un sottoinsieme B, si chiama COMPLEMENTARE di B rispetto ad A, l’insieme che si ottiene come differenza fra A e B.
Se B⊆A, l’insieme complementare di B rispetto ad A è A-B.
Esempi
- A={1,2,3,4 } B={1,2 } A-B={3,4 }
- Se A={x/x cittadino europeo } B={x/x cittadino europeo abitante in Spagna }. L’insieme di tutti i cittadini europei che non abitano in Spagna costituisce un insieme complementare quindi: A-B={x/x cittadino europeo che non abita in Spagna }.
- Se A è l’insieme delle lettere di una parola e B quello delle sue consonanti,
è l’insieme delle vocali della parola.
- Il complementare di un insieme può essere vuoto. Per esempio, è sempre vero che
= ∅.
IL PRODOTTO CARTESIANO
Il prodotto cartesiano di due insiemi A e B è l’insieme formato da tutte le coppie ordinate (a;b) in cui il primo elemento appartiene al primo insieme A e il secondo elemento al secondo insieme B. C=AxB={(a;b)| a∈ A e b ∈ B}.
Il prodotto cartesiano fra due insiemi non è commutativo. AxB ≠ BxA
Per esempio a un torneo di scacchi partecipano tre ragazzi italiani, Paolo, Carlo e Elena, che costituiscono l’insieme A={p,c,e} e due ragazzi russi, Boris e Svetlana, che formano l’insieme B={b,s}.
Indichiamo le coppie che si formano in modo che il primo elemento sia di nazionalità italiana e il secondo di nazionalità russa:
(Paolo, Boris) (Carlo, Boris) (Elena, Boris)
(Paolo, Svetlana) (Carlo,Svetlana) (Elena,Svetlana)
Consideriamo l’insieme C che ha per elementi tutte le coppie ordinate dei loro nomi:
C={(p,b),(c;b),(e;b),(p;s),(c;s),(e;s)} e scriviamo C=A x B dove C è il prodotto cartesiano di A x B
Esercizio
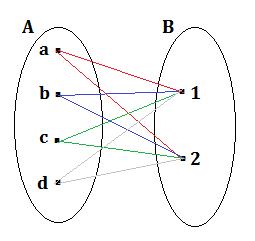
Rappresenta il prodotto cartesiano A x B degli insiemi: A = {a,b,c,d} e B ={1 , 2}
La rappresentazione per elencazione è:
A x B = {(a; 1), (a; 2), (b ; 1), (b; 2), (c; 1), (c; 2), (d; 1), (d; 2) }
La rappresentazione con una tabella a doppia entrata è :
| A x B | 1 | 2 |
| a | (a;1) | (a; 2) |
| b | (b;1) | (b; 2) |
| c | (c; 1) | (c; 2) |
| d | (d; 1) | (c; 2) |
La rappresentazione sagittale è :
La rappresentazione cartesiana o diagramma cartesiano, del prodotto cartesiano è una rappresentazione grafica che utilizza due semirette fra loro perpendicolari.
Sulla semiretta orizzontale rappresentiamo gli elementi del primo insieme, su quello verticale del secondo insieme.
Da ogni elemento del primo insieme tracciamo una semiretta verticale, da ogni elemento del secondo insieme tracciamo una semiretta orizzontale.
Queste semirette formano una griglia, i punti d’incontro rappresentano le coppie del prodotto cartesiano.