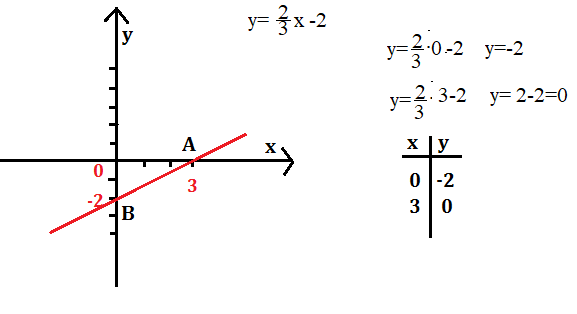Un retta che non passa per l’origine avrà equazione y=mx+q dove m è il coefficiente angolare e q è il termine noto ed è l’ordinata del punto d’intersezione della retta con l’asse delle y.
Se q=0 la retta passa per l’origine degli assi.
Per disegnare una retta non passante per l’origine, poichè per due punti passa una sola retta, si possono trovare le coordinate solo dei due punti.
Ad esempio volendo disegnare la retta di equazione y=2\3 x -2 si fa uno schemino e si attribuiscono ad x dei valori a cui corrisponderanno determinati valori di y.
Avremo cioè i punti A(0,-2); B(+3,0) ed il diagramma sarà la retta AB.
Esercizio n 1
Costruisci la tabella dei valori per ciascuna funzione matematica.
a) y = 3\2 x – 2
Per costruire la tabella dei valori si attribuiscono alla variabile x alcuni valori e si calcolano i corrispondenti valori della y.
| x | y |
| -2 | -5 |
| 0 | -2 |
| +2 | +1 |
| +4 | +4 |
Per x = -2 si ottiene: y = 3\2 · (-2) -2 = – 3 – 2= -5
Per x = 0 y = 3\2 · 0 – 2 = – 2
Per x = +2 y = 3\2 · (+2) – 2 = 3 – 2 = +1
Per x = + 4 y = 3\2 · ( +4) – 2 = 6 – 2 = + 4
b) y = 3 – x²
| x | y |
| -2 | -1 |
| -1 | +2 |
| 0 | +3 |
| +1 | +2 |
| +3 | -6 |
Per x = -2 y = 3 – (-2)² = 3 – 4 = -1
Per x = -1 y = 3 – (-1)² = 3 – 1 = +2
Per x = 0 y = 3 – (0)² = +3
Per x = +1 y = 3 – (+1)² = 3 – 1 = +2
Per x = +3 y = 3 – (+3)² = 3 – 9 = – 6
Esercizio n° 2
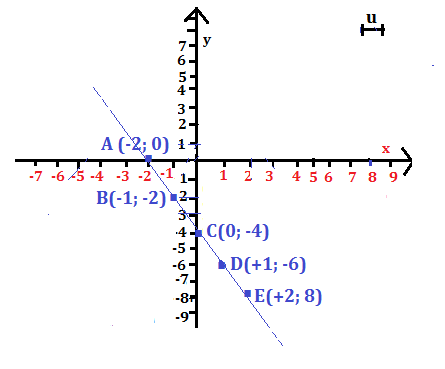
Disegna il grafico e riconosci le caratteristiche della funzione y = -2x -4, evidenziando quali sono le coordinate del punto di intersezione con l’asse y.
La tabella dei valori è:
| x | -2 | -1 | 0 | +1 | +2 |
| y | 0 | -2 | -4 | -6 | -8 |
La funzione è una retta non passante per l’origine, con equazione tipo: y = mx + q.
Il suo coefficiente angolare è:
m = -2 quindi è il coefficiente di x
La retta interseca l’asse y nel punto C (0; -4), l’ordinata di tale punto coincide con il termine noto dell’equazione: q=- 4 è l’ordinata del punto d’intersezione con l’asse y
Esercizio n° 3
Stabilisci, senza ricorrere alla rappresentazione grafica, quale tra i due punti A(-2; +3) e B (-1; +4) appartiene alla retta y= -3x + 1.
Sostituendo le coordinate del punto A nell’equazione della retta si ottiene:
+3 = -3(-2) +1 +3 = +6 +1 +3 = +7
L’uguaglianza non è vera, pertanto il punto A non appartiene alla retta.
Sostituendo le coordinate del punto B si ottiene:
+4 = -3(-1) +1 +4 = +3 +1 +4 = +4
L’uguaglianza è vera, quindi il punto B appartiene alla retta.