Si dice che un corpo è in equilibrio quando è fermo e rimane fermo nonostante siano esercitate su di esso delle forze.
A volte il corpo che vogliamo analizzare è così piccolo rispetto all’ambiente in cui può muoversi da essere considerato come un punto, detto punto materiale perchè a differenza di un punto geometrico è dotato di una massa.
Quindi in definitiva possiamo dire che un punto materiale è privo di dimensioni ma ha una massa , cioè quella dell’oggetto che rappresenta.
Un punto materiale non avendo dimensioni, l’unica cosa che può fare è traslare, quindi non può ruotare nè deformarsi.
Esso quindi è un modello che viene usato per descrivere in modo semplificato il comportamento di un oggetto.
Ci sono alcune situazioni in cui questo modello non può essere usato perchè le dimensioni dell’oggetto sono troppo grandi per essere trascurate, come nel caso di una palla da basket rispetto alle dimensioni del canestro, in questo caso si usa un altro modello e cioè quello del corpo rigido.
Esso è un oggetto esteso che può traslare e ruotare , ma che non viene deformato, qualsiasi siano le forze applicate.
Il peso di un corpo rigido lo si può considerare come l’insieme di molti punti materiali sui quali agisce la forza peso, quindi il peso del corpo rigido è la somma vettoriale dei peso dei singoli punti.
Quindi punto materiale e corpo rigido sono dei modelli perchè non esistono corpi realmente indeformabili.
L’EQUILIBRIO DEL PUNTO MATERIALE
Un punto materiale rimane fermo cioè in equilibrio statico , quando la risultante delle forze che agiscono su di esso è nulla.
Tale equilibrio si rompe non appena la risultante delle forze che agiscono su di esso diventa zero.
LE FORZE VINCOLARI
L’equilibrio di qualsiasi oggetto appeso o poggiato su un ripiano dipende dalla presenza di vincoli.
Un vincolo è un oggetto, cioè un corpo fisso che impedisce a un altro corpo di compiere alcuni movimenti; esercitando su di esso una forza chiamata reazione vincolare.
Il pavimento sotto i nostri piedi è un vincolo così come il piano di un tavolo ecc.
La forza vincolare di un piano applicata da un vincolo è sempre perpendicolare al piano con un verso tale da respingere l’oggetto, invece quella di una corda è sempre parallela alla corda e ha verso tale da tirare l’oggetto.
Quando siamo fermi in piedi in mezzo ad una stanza, su di noi agisce la forza peso che tenderebbe a farci andare verso il basso, questo non avviene perchè il pavimento, cioè il vincolo, agisce su di noi con una forza uguale e contraria detta appunto forza vincolare uguale ed opposta alla forza peso. Alla fine rimaniamo in equilibrio perchè la somma vettoriale delle forze che agiscono su di noi è nulla.
Tutti i vincoli però si rompono se sono sottoposti a forze eccessive.
EQUILIBRIO SU UN PIANO ORIZZONTALE
La situazione più comune che riscontriamo ogni giorno è l’equilibrio di un oggetto appoggiato su un piano orizzontale.
Consideriamo un oggetto posto sul pavimento, esso sarà sottoposto alla forza peso che lo spingerà verso il basso, ma nonostante ciò l’oggetto è fermo, questo perchè contemporaneamente il pavimento lo sottoporrà a una forza detta vincolare uguale e contraria alla forza peso che lo spinge verso l’alto .
Poichè l’oggetto è in equilibrio, vorrà dire che la somma delle forze dovrà essere nulla quindi:
Riassumendo possiamo dire che il pavimento agisce sull’oggetto con una forza uguale e contraria alla forza peso.
In pratica la forza vincolare detta anche reazione vincolare, esercitata da una superficie ha direzione perpendicolare alla superficie, verso uscente dalla superficie e modulo uguale alla forza permanente che agisce sulla superficie.
L’EQUILIBRIO SUL PIANO INCLINATO
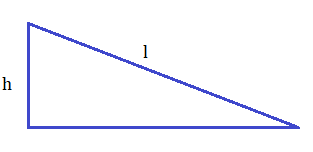
Consideriamo un piano inclinato di lunghezza l ed altezza h, con attrito trascurabile. Poniamo sopra a tale piano un carrello con un vaso in equilibrio e vediamo quale forza dobbiamo applicare affinchè tale oggetto non si muova.
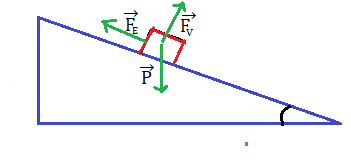
Vediamo le forze che agiscono sul carrello: forza peso verso il basso, forza vincolare verso l’alto e perpendicolare al piano inclinato e la forza equilibrante che mantiene in equilibrio il corpo.
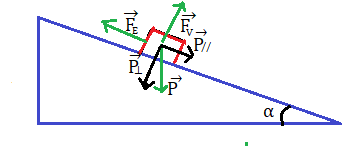
A questo punto scomponiamo la forza peso nelle sue componenti cioè il vettore forza peso perpendicolare e parallelo al piano inclinato: e
. In pratica è com e se introducessimo un sistema di riferimento cartesiano , dove l’asse delle x rappresenta la componente parallela e l’asse delle y la componente perpendicolare.
All’equilibrio il carrello non si muove quindi vuol dire che tutte le forze si bilanciano. Vorrà dire che la forza vincolare è bilanciata dalla forza perpendicolare e la forza equilibrante è bilanciata dalla forza parallela. Se il carrello si muovesse vorrà dire che la forza parallela è maggiore della forza equilibrante.
A questo punto le componenti della forza peso le possiamo andare a calcolare con le regole della trigonometria in quando in un triangolo rettangolo un cateto è uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto oppure al prodotto dell’ipotenusa per il coseno dell’angolo adiacente quindi:
Ma possiamo arrivare a fare un’altra affermazione è cioè: il seno di alfa, considerando la formula opposta , è il rapporto tra h che è un cateto e l che è l’ipotenusa quindi
Quanto più il piano è inclinato, maggiore sarà il rapporto tra h ed l e di conseguenza maggiore sarà la forza equilibrante da applicare per mantenere il corpo in equilibrio.
Il rapporto h\l è la pendenza o inclinazione del piano inclinato; è un numero positivo minore di 1 quindi la forza equilibrante che è uguale alla forza peso parallela è un valore sempre più piccolo della forza peso.