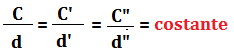Se vogliamo misurare la lunghezza di una circonferenza dobbiamo confrontare con un segmento, scelto come unità di misura. E’ evidente che non è possibile un confronto diretto poichè la circonferenza è una linea curva e il segmento è una parte di una linea retta.
Prendiamo un filo flessibile, e disponiamolo lungo una circonferenza in modo che vi aderisca. Stendiamo poi il filo ottenendo così il modello di un segmento: diremo che questo segmento rappresenta la circonferenza rettificata.
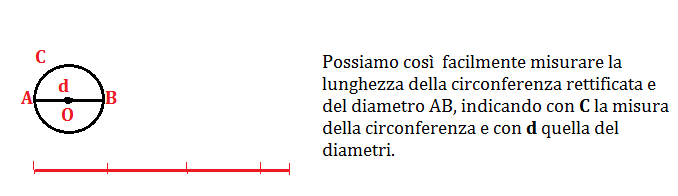
Quindi: per lunghezza di una circonferenza si intende la lunghezza del segmento che rappresenta la circonferenza rettificata.
In modo analogo possiamo misurare la lunghezza di:
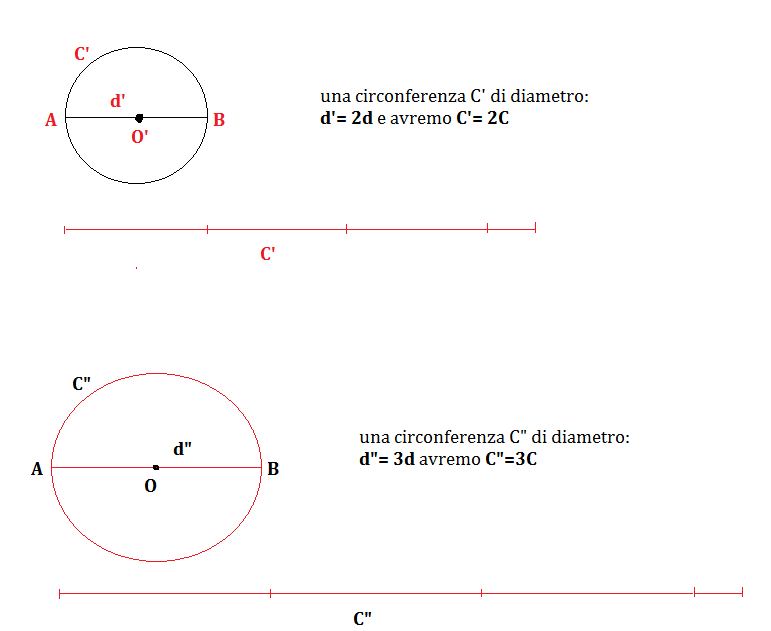
Quindi la lunghezza di una circonferenza e quella del suo diametro sono grandezze direttamente proporzionali e il rapporto tra le misure è costante:
Il rapporto tra la misura di una circonferenza e quella del suo diametro è costante.
Il valore di questo rapporto si indica con la lettera π (pi greco) e corrisponde a un numero decimale illimitato non periodico (un numero irrazionale)
π= 3,14159265358….
Abitualmente usiamo solo il valore approssimato per difetto a meno di 0,01:
π= 3,14
Possiamo quindi scrivere la formula
da cui si ottiene:
C= π · d ma d= 2r quindi: C= π · 2r
da cui si ricavano le formule inverse che permettono di trovare la lunghezza del diametro o del raggio data la misura della circonferenza:
e