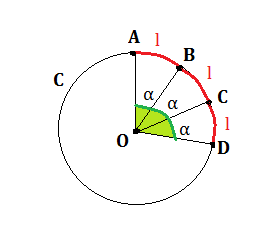
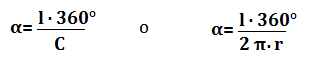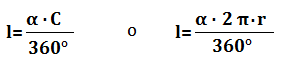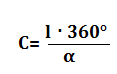Disegniamo una circonferenza C di centro O e raggio r, fissiamo su di essa un arco AB di lunghezza l e indichiamo con α l’ampiezza del corrispondente angolo al centro.
Poichè ad archi congruenti corrispondono angoli al centro congruenti, se raddoppiamo o triplichiamo la lunghezza dell’arco AB anche i corrispondenti angoli al centro diventeranno il doppio o il triplo di α. Se l’arco coincide con l’intera circonferenza, allora l’angolo al centro corrispondente diventerà 360°.
| misura dell’arco | misura dell’angolo α |
| l | α |
| 2 l | 2 α |
| 3 l | 3 α |
| C | 360° |
Le due grandezze, lunghezza dell’arco e ampiezza dell’angolo al centro, sono direttamente proporzionali.
Possiamo scrivere la seguente proporzione:
l : C = α : 360°
poichè C= 2π · r si ottiene:
l : 2 π r = α : 360°
Dalla proporzione precedente si ricava:
- l’ampiezza dell’angolo al centro α noti la lunghezza dell’arco l e la misura della circonferenza C:
- la lunghezza dell’arco l conoscendo l’ampiezza dell’angolo α e la lunghezza della circonferenza C.
- la misura di C conoscendo l’ampiezza dell’angolo α e la lunghezza dell’arco l:
La lunghezza di un arco di circonferenza si ottiene dividendo la lunghezza della circonferenza per 360° e moltiplicando il risultato per l’ampiezza dell’arco espressa in gradi.