Operazioni nell’insieme dei numeri interi
ADDIZIONE DI NUMERI RELATIVI
Sulla retta numerica il segno + dell’addizione significa spostarsi verso destra, il segno – significa spostarsi verso sinistra. Se il primo segno è + e il secondo è -, si invertirà il segno del secondo numero, se il primo numero è + e il secondo è + si conserverà lo stesso verso.
SOMMA DI DUE NUMERI CONCORDI
La somma di due numeri concordi è un numero che ha:
- per valore assoluto la somma fra i valori assoluti;
- per segno lo stesso dei due numeri.
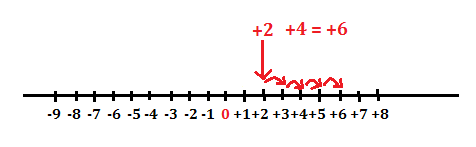
(+2)+(+4)=+6
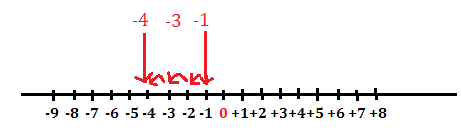
(-1)+(-3)=-4
SOMMA DI DUE NUMERI DISCORDI
La somma di due numeri discordi è un numero che ha:
- per valore assoluto la differenza fra il maggiore e il minore dei valori assoluti;
- per segno quello del numero che ha valore assoluto maggiore.
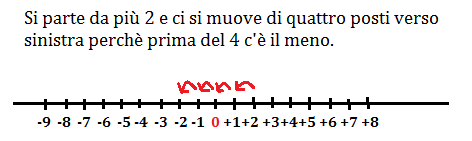
(+2)+(-4)=-2
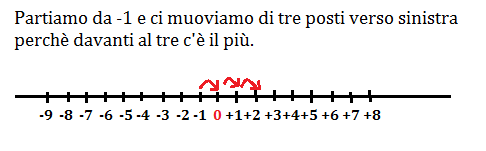
(-1)+(+3)=+2
La somma di due numeri relativi opposti è zero: ( +6)+ (-6)=0
SOTTRAZIONE TRA NUMERI RELATIVI
Si può sempre eseguire la sottrazione di due numeri reali e il risultato è ancora un numero reale. Questa proprietà si chiama chiusura di R rispetto alla sottrazione.
La differenza di due numeri interi è la somma del minuendo con l’opposto del sottraendo.
Sulla retta numerica il risultato della sottrazione di due numeri relativi si trova partendo dal minuendo e spostandosi:
- Verso sinistra, se il sottraendo è positivo
- Verso destra, se il sottraendo è negativo
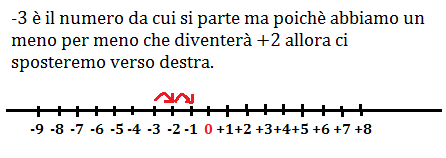
(-3)-(-2) =-1
(+5)-(+4)=+1
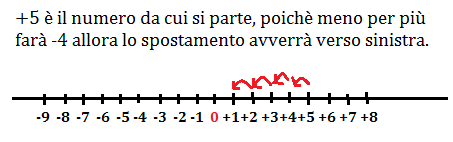
Quindi si può dire che la differenza tra due numeri relativi, si ottiene addizionando al minuendo l’opposto del sottraendo +5 –(-6)= +5 +6=11.
LA MOLTIPLICAZIONE
Il prodotto di due numeri relativi è il numero relativo che:
- Ha per modulo il prodotto dei moduli dei singoli fattori;
- È positivo se i fattori sono concordi cioè dello stesso segno (-)·(-)=+; (+)·(+)=+;
- È negativo se i fattori sono discordi (-)·(+)=-; (+)·(-)=-;
(-5)·(+6)= -30; (+7)·(-6)=-42; (+9)·(+9)=+81; (-6)·(-6)=+36
Il prodotto di più fattori è un numero relativo che ha:
- Per modulo il prodotto di tutti i moduli;
- È positivo se i segni – sono in numero pari +-+—;
- È negativo se i segni – sono in numero dispari +-+-+-;
Esempio: (+2)·(-6)·(-1)·(+2)=+24 infatti i segni meno sono in numero pari.
(-2)·(-6)·(-1)·(+2)= -24 infatti i segni meno sono in numero dispari.
Se uno dei fattori è 0 il prodotto è 0.
Il prodotto di due fattori di cui uno è +1, è uguale all’altro fattore, invece il prodotto di due fattori di cui uno è -1, è uguale all’opposto dell’altro fattore.
LA DIVISIONE
Il quoziente di due numeri relativi è un numero relativo che:
- Ha per modulo il quoziente dei moduli;
- È positivo se dividendo e divisore sono concordi, cioè dello stesso segno;
- È negativo se dividendo e divisore sono discordi, cioè sono diversi.
+10:(-2)=-5; -8: (-4)=+2; +20:(+10)=+2
Anche per le espressioni con i numeri relativi la moltiplicazione e la divisione hanno la priorità sul + e sul -. I calcoli tra parentesi vanno svolti sempre prima.
Il quoziente dei numeri relativi si ottiene moltiplicando il primo per il reciproco del secondo:
Esempi: