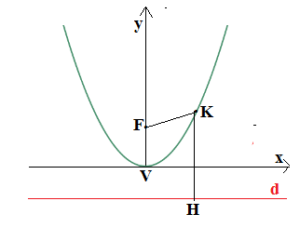
Consideriamo il caso in cui la parabola abbia l’asse si simmetria coincidente con l’asse y e che l’origine quindi O(0,0) coincida con il vertice.
La direttrice ovviamente si troverà al di sotto dell’asse delle x, quindi avrà equazione y=-p
Diciamo che il fuoco (F) ha coordinate (0,p) quindi la direttrice avendo la stessa distanza di F dal vertice V avrà come equazione y = -p
Il punto K avrà come coordinate (x,y).
Sappiamo poi che per definizione K appartiene alla parabola se e solo se KF=KH.
A questo punto calcoliamoci i due segmenti:
poniamo KF=KH quindi otteniamo
A questo punto eleviamo entrambi i membri al quadrato perchè tutti e due positivi. Otteniamo:
otteniamo:
visto che l’espressione è un valore numerico conosciuto, lo possiamo indicare con a quindi sostituendolo otteniamo:
y=ax²
Viato che
A questo punto possiamo riassumere dicendo che una parabola con vertice nell’origine degli assi e asse di simmetria coincidente con l’asse y ha equazione :
y=ax² con a≠0
Il fuoco è il punto:
F (0, )
La direttrice è la retta:
A questo punto per disegnare una parabola dobbiamo prima di tutto trovare le coordinate di altri punti della parabola , quindi attribuiamo dei valori alla variabile x per sapere quanto varrà la y. Generalmente lo si fa per tre volte.
Poi bisogna vedere se il valore della a è positivo o negativo.
Se a >0 tutti i valori della parabola hanno ordinate positive e quindi il grafico è contenuto interamente nei quadranti positivi degli assi e si dirà che la parabola volge la concavità verso l’alto.
Se a<0 tutti i punti hanno ordinate negative ed il grafico è interamente contenuto nel semipiano negativo e si dice che la parabola volge la concavità verso il basso.
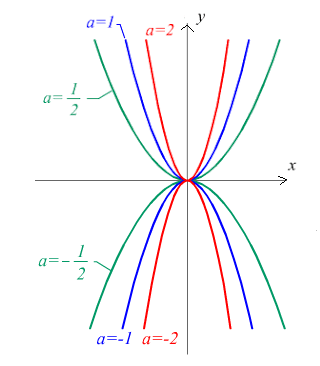
Un’altra cosa che si può dire sul valore della a è :
al crescere di a in valore assoluto, la parabola diventa sempre più stretta. La rappresentazione grafica rende bene l’idea di quello che accade.
ESEMPIO
Data la parabola , determinare le coordinate del fuoco e l’equazione della direttrice e rappresentarla graficamente.
L’equazione è del tipo y= ax² quindi F(0; ) , visto che a =
quindi F(0,1).
Inoltre quindi y=-1
A questo punto per costruire il grafico della parabola dobbiamo trovare le coordinate di qualche punto.
La parabola avrà concavità verso l’alto perchè a>0.
Programma matematica terzo superiore