Un poligono si dice inscritto in una circonferenza se tutti i suoi vertici sono punti della circonferenza. La circonferenza si dice circoscritta al poligono e il suo centro si dice circocentro del poligono.
A un poligono si può circoscrivere una circonferenza se gli assi di tutti i suoi lati si incontrano in un unico punto: in questo caso il poligono si dice inscrivibile.
I triangoli, i quadrati, i rettangoli, i trapezi isosceli e tutti i poligoni regolari sono inscrivibili.
Consideriamo un generico poligono ABCDE inscritto nella circonferenza C.
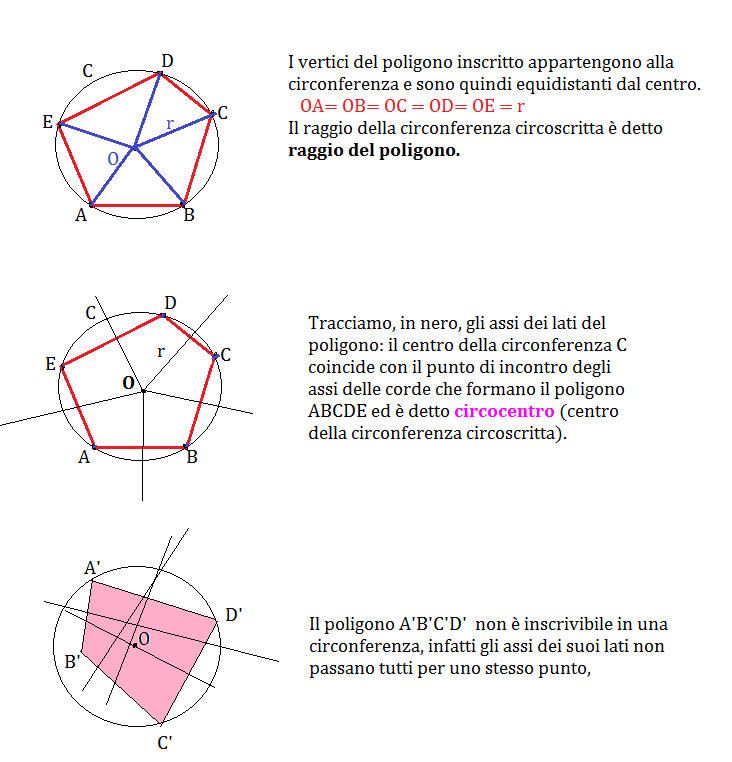
OSSERVAZIONI
Già sappiamo che un angolo inscritto in una semicirconferenza è un angolo retto e quindi un triangolo rettangolo è inscrivibile in una semicirconferenza il cui diametro è l’ipotenusa del triangolo rettangolo. Di conseguenza, il circocentro di un triangolo rettangolo è il punto medio O dell’ipotenusa.
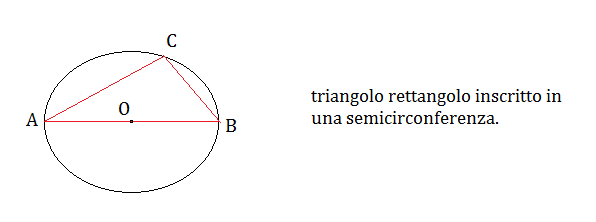
Consideriamo ora il triangolo rettangolo ABC inscritto in una circonferenza, l’ipotenusa AB è il diametro della circonferenza e la mediana CO relativa all’ipotenusa del triangolo rettangolo è un raggio della circonferenza.
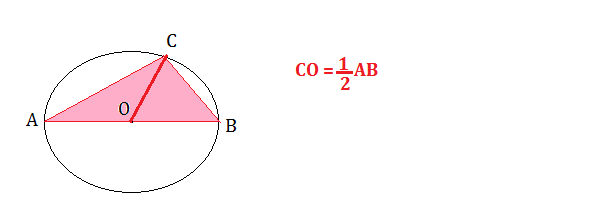
La mediana relativa all’ipotenusa di un triangolo rettangolo è la metà dell’ipotenusa.