La proporzionalità diretta e inversa si applicano per risolvere molti problemi pratici. Se nel problema figurano tre valori di grandezze direttamente proporzionali e si vuole trovare il quarto si ha un problema del tre semplice diretto, se le grandezze sono inversamente proporzionali si ha un problema del tre inverso.
PROBLEMI DEL TRE SEMPLICE DIRETTO
PROBLEMA 1
Per preparare una torta al cioccolato per 8 persone si usano 200 g di cioccolato fondente. Quanto cioccolato fondente occorre per preparare la stessa torta per 14 persone?
Le grandezze coinvolte nel problema sono due : la quantità di cioccolato (in g) e il numero di persone. Esse sono direttamente proporzionali poichè raddoppiando o triplicando il numero di persone raddoppia o triplica la quantità di cioccolato, il loro rapporto è costante :
.
Si predispone uno schema in cui si trascrivono i 3 dati noti e l’incognita x del problema. Si inseriscono due frecce: una che va dalla x verso il termine noto e l’altro con lo stesso verso poichè le due grandezze sono direttamente proporzionali.
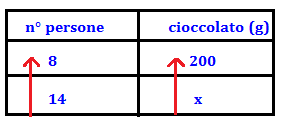
Seguendo il verso delle frecce riportate in tabella, si può scrivere la proporzione risolutiva del problema:
14 :8= x:20 da cui
quantità di cioccolato da usare.
PROBLEMA 2
Un campanile alto 24 metri proietta un’ombra di 32 metri. Qual è la lunghezza di un’ombra proiettata da un palo alto 9 metri?
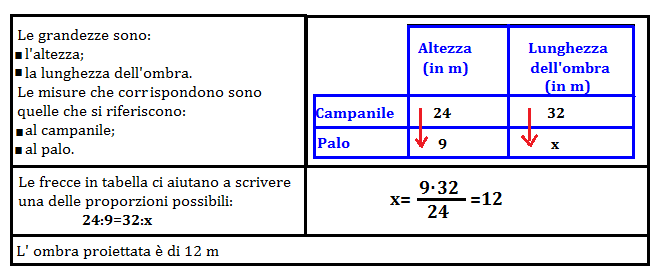
L’altezza del campanile e la lunghezza dell’ombra sono grandezze direttamente proporzionali, poichè se raddoppia o triplica l’altezza del campanile, raddoppia o triplica anche la lunghezza dell’ombra proiettata. Una volta inserite le grandezze note e l’incognita in una tabella con frecce nello stesso verso essendo grandezze direttamente proporzionali, possiamo ricavare la proporzione finale e quindi la x.
PROBLEM N° 3
A uno spettacolo di beneficenza erano presenti 800 persone per un incasso di 9600 euro.
Alla replica dello spettacolo si è avuto un incasso di 8640 euro. Quante persone erano presenti al secondo spettacolo se il prezzo d’imgresso è rimasto invariato?

PROBLEMA N° 4
Una pompa può aspirare 12 l di acqua in 6 secondi. Quanti litri di acqua può aspirare in 15 secondi?
Si tratta di grandezze direttamente proporzionali perchè se raddoppia o triplica il tempo a disposizione per aspirare l’acqua, raddoppia o triplica anche la quantità d’acqua aspirata.
Chiamiamo x la quantità d’acqua aspirata in 15 secondi.

PROBLEMA N° 5
In un negozio del Canton Ticino è esposta una camicia che costa 24 franchi svizzeri. Sapendo che oggi il franco svizzero vale 0,62 euro, calcola quanto costa la camicia in euro.
La quantità di franchi svizzeri e di euro sono grandezze direttamente proporzionali.
Conosciamo il cambio unitario, ossia il cambio in euro di un franco svizzero, e vogliamo calcolare il cambio totale x.

PROBLEMA N° 6
Un lettore mp3 venduto su un sito internet statunitense costa 200 dollari. Sapendo che un dollaro statunitense vale circa o,69 euro, quanto costa in euro il lettore?
Vedi problemi del tre semplice inverso
Programma matematica seconda media
