La proporzionalità diretta e inversa si applicano per risolvere molti problemi pratici. Se nel problema figurano tre valori di grandezze direttamente proporzionali e si vuole trovare il quarto si ha un problema del tre semplice diretto, se le grandezze sono inversamente proporzionali si ha un problema del tre inverso.
PROBLEMI DEL TRE SEMPLICE INVERSO
PROBLEMA 1
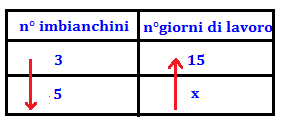
Per dipingere le pareti di 12 appartamenti, 3 imbianchini impiegano 15 giorni. Quanti giorni occorreranno a 5 imbianchini per portare a termine lo stesso lavoro ?
Le grandezze coinvolte sono due: il numero d’imbianchini e il numero di giorni di lavoro. Esse sono inversamente proporzionali perchè raddoppiando o triplicando il numero d’imbianchini i giorni di lavoro diventeranno 1\2 , 1\3 di quelli iniziali, il loro prodotto è costante 3 · 15= 5 · x
Nello schema di sotto sono stati riportati i dati del problema con l’incognita x, le frecce di verso contrario indicano che le due grandezze sono inversamente proporzionali. Quindi seguendo il verso delle frecce si ottiene la proporzione risolutiva del problema e cioè 3: 5= x : 15 da cui x = = 9 n° di giorni che occorrono ai 5 imbianchini.
PROBLEMA 2
Una scala che sale al secondo piano di una casa è formata da 32 scalini alti 18 centimetri. Quanti gradini dovrebbe avere la stessa scala se l’altezza del gradino fosse di 16 centimetri?
Le grandezze altezza dello scalino e numero di scalini sono inversamente proporzionali, quindi inseriamo queste grandezze nella tabelle con le frecce orientate in verso opposto.
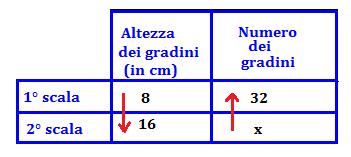
la proporzione sara 18 :16= x : 32 ⇒
.
Quindi occorrono 36 gradini alti 16 cm.
PROBLEMA N° 3
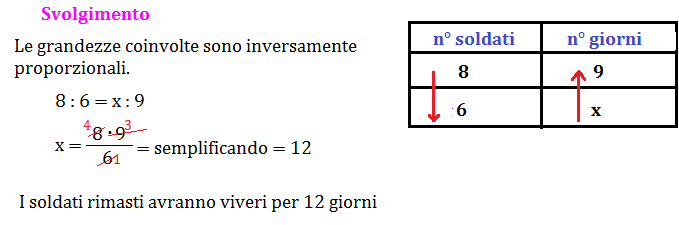
A un gruppo di 8 soldati impegnati in una perlustrazione in montagna vengono0 consegnati viveri per 9 giorni. Prima della partenza 2 soldati sono destinati ad altro incarico. In quanti giorni i 6 soldati rimasti consumeranno la stessa quantita di viveri?
PROBLEMA N° 4
Un libro ha 180 pagine e 42 righe per pagina. Quante pagine avrebbe lo stesso libro se ogni pagina avesse 36 righe?
Le grandezze che compaioni nel problema sono inversamente proporzionali, perchè se raddioppasse il numero di righe per pagina basterebbe la metà delle pagine per la scrittura del libro. Se le righe per pagina fossero la metà di quelle date raddoppierebbe il numero delle pagine necessarie. Indichiamo con x il numero di pagine necessarie se ogni pagina avesse 36 righe.
Vedi problemi del tre semplice diretto
