Non è possibile stabilire delle regole precise ma ci sono delle regole generiche da poter considerare:
- Si fissa l’incognita;
- si traduce il problema in equazione, cioè si stabilisce una relazione fra gli elementi noti e gli elementi incogniti;
- si risolve l’equazione;
- si esaminano le radici trovate, cioè si verifica se le radici trovate possono essere soluzioni del problema. Per questa ultima fase bisogna tener presente che: se l’incognita esprime un numero di persone o un numero di oggetti, si accettano solo le soluzioni espresse da numeri interi positivi. Se l’incognita esprime la misura di un segmento o di un’area, o di un volume,….si accettano solo le radici espresse da numeri positivi.
Programma matematica terza media
PROBLEMI
1) Trovare un numero la cui metà aumentata di 6 dia 9.
trovare un numero x
la cui metà
aumentata di 6
dia 9
quindi questa è l’equazione da risolvere, facciamo poi il minimo comune multiplo
⇒x+12=18⇒ x=18-12⇒ x=6.
2) Un uomo di 44 anni ha un figlio di 6 anni: fra quanti anni il padre avrà un’età tripla del figlio?
Anni del padre 44
Età del figlio 6
Anni del padre fra x anni 44+x
Anni del figlio tra x anni 6+x
equazione finale 44 + x= 3(6+x) età del figlio quando il padre avrà il triplo della sua età.
44 + x= 18 + 3x ⇒ x – 3x= -44 + 18
-2x = -36 ⇒
x=13
Risposta: fra 13 anni l’età del padre sarà tre volte quella del figlio.
3) Determinare due numeri naturali sapendo che la loro somma è 154 e che uno è tre quarti dell’altro.
la somma dei due numeri naturali è x+y= 154
uno è i 3\4 dell’altro quindi x=3\4y
L’equazione da risolvere è x+y=154 ma sostituendo x=3\4y avremo:
x=3\4y+y=154 ⇒
quindi 7y=616
y=88 e x=154-88⇒ x=66
4) Determinare un numero naturale il cui triplo aumentato di due sia 187.
trovare un numero naturale x
il cui triplo 3x
aumentato di 2 3x+2
dia 187 3x+2=187
La risoluzione dell’equazione è 3x=187-2⇒ 3x= 185
la soluzione non è accettabile perchè la frazione non è un numero naturale.
5) Trovare un numero il cui triplo diminuito di 5 è uguale al numero stesso aumentato di 3.
trovare un numero x
il cui triplo 3x
diminuito di 5 3x-5
sia uguale x+3
Quindi l’equazione da svolgere sarà 3x-5=x+3
3x-x=+3+5 ⇒ 2x=8
Il numero cercato è +4.
6) In una scuola il numero degli alunni supera di 128 i 4\5 del numero delle alunne e la loro differenza è 40. Calcolare il numero complessivo degli alunni della scuola.
numero delle alunne x
numero degli alunni 4\5 x +128
la differenza tra alunni e alunne è 40 quindi ( 4\5x +128)-x=40 sarà l’equazione da svolgere
eliminando il denominatore
4x+640-5x=200⇒ -x=-440 ⇒ x=440
Il numero delle alunne è 440 quindi il numero degli alunni sarà dato da 440+40=480 e il numero complessivo sarà dato da 440+480=920
7) In una scuola frequentata da 900 alunni quelli che studiano la lingua inglese sono i 5\3 di quelli che studiano la lingua francese. Calcolare il numero degli alunni che studiano ciascuna lingua.
alunni che studiano la lingua francese x
alunni che studiano la lingua inglese 5\3 x
alunni totali x+ 5\3 x=900 quindi questa è l’equazione che dobbiamo risolvere
eliminiamo il denominatore e avremo:
3x+5x=2700 ⇒ 8x= 2700 x=2700\8 =337,5 ma tale valore non può essere accettato come soluzione perchè è un valore decimale e quindi non può rappresentare il numero di alunni. Quindi il problema è impossibile.
8) In un rettangolo il perimetro è di 80 cm e l’altezza è i 2\3 della base. Calcolare la lunghezza dei lati e l’area del rettangolo.
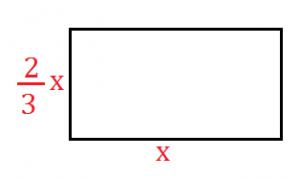
la base sarà la nostra x
l’altezza sarà 2\3 x
il perimetro di un rettangolo è uguale alla somma della base per due e dell’altezza per due quindi poichè la misura del perimetro del rettangolo è 80, si ha l’equazione 2·x+2(2\3 x)=80
eliminando il denominatore
6x+4x=240⇒ 10x=240⇒ x=240\10 ⇒ x=24
Si ha perciò AB=24cm BC=(2\3 •24 )= 16 cm
9) Il triangolo ABC ha il perimetro di 130m. Calcolare la misura dei lati, sapendo che AB è 3\4 di AC e BC è 4\7 di AC.

p=130m; AC=x ; AB=3\4 x; BC=4\7 x.
Il perimetro del triangolo è uguale alla somma dei tre lati quindi:
AB+BC+AC=130⇒ x+3\4x+4\7= 130
eliminiamo il denominatore
28x + 21x + 16x = 3640
65x = 3640
x= 65
AC=56m; AB =3\4x ⇒ AB= 3\4 ·56=42m; BC=4\7 ⇒BC=4\7·56=32m
10) Un numero naturale aggiunto al suo triplo è uguale a 76. Qual è il numero?
Dati Incognite
n = numero naturale n = x
n + 3n = 76 x = ?
Equazione risolvente
x + 3x = 76
4x = 76 ⇒ x = 76\4 = 19
Verifica
1° membro 2° membro
19 + 3 · 19 = 19 + 57 = 76 76
La soluzione è accettabile perchè 19 è un numero naturale.
11) Aggiungendo 5 al doppio di un numero naturale si ottiene come risultato 20. Qual è il numero?
Dati Incognite
n = numero naturale n = x
2n +5 = 20 x =?
Equazione risolvente
2x + 5 = 20
quindi 2x = 20 – 5
2x = 15 ⇒ x = 15\2
Verifica
1° membro 2° membro
2 · 15\2 + 5 = 20 20
La soluzione non è accettabile perchè 15\2 non è un numero naturale.
12) Un numero triplo dell’altro
Se i due numeri sono e
, si può indicare
con x e si ottiene:
= x ;
= 3x
13) Due numeri la cui somma è 40.
Se = x, si può indicare
con 40 – x, quindi:
= x;
= 40 – x
14) Due numeri consecutivi.
Ponendo = x, si ottiene:
= x + 1
15) Tre numeri consecutivi.
Se ,
,
sono i tre numeri, con
<
<
, indicando
con x si ottiene:
= x- 1;
= x;
= x + 1
16) Due numeri pari (o dispari) consecutivi.
Se = x;
= x + 2
17) Tre numeri pari (o dispari) consecutivi.
Se ,
,
sono i tre numeri, con
<
<
, indicando
con x si ottiene:
= x- 2;
= x;
= x + 2
18) Determina due numeri naturali, sapendo che la loro somma è 30 e che 5\6 del primo superano di 3 il secondo.
Dati Incognite
+
= 30
= x
5\6 =
+ 3
ed
= numeri naturali
= 30 – x
Equazione risolvente
5\6 x = 30 – x + 3
6 · 5\6 x = 6 · 30 – 6 · x + 6 · 3
5x = 180 – 6x + 18
11x = 198
x = 198\11 ⇒ x = 18
Verifica
1° membro 2° membro
5\6 · 18 = 15 30 – 18 + 3 = 15
= 18
= 30 – 18 = 12
La soluzione è accettabile perchè i due numeri sono naturali.
19) La somma di tre numeri pari consecutivi è 84. Determina i tre numeri.
Dati Incognite
+
+
= 84
,
,
= ?
,
,
= numeri pari
Svolgimento
Posto = x, si ottiene:
= x – 2 e
= x + 2
Equazione risolvente
X – 2 + X + X + 2 = 84
3x = 84
quindi:
x = 84\3 ⇒ x = 28
Verifica
1° membro 2° membro
28 – 2 + 28 + 28 + 2 = 84 84
si ottiene:
= 28 – 2 = 26
= 28
= 28 + 2 = 30
La soluzione è accettabile perchè i tre numeri sono pari.
20) Tre amici si dividono una vincita al lotto di 1640 euro, in modo che il primo e il terzo abbiano rispettivamente il doppio e la terza parte di quanto riceve il secondo. Quale somma riceve ciascuno dei tre amici?
Dati Incognite
Vincita = 1640 euro somma del secondo = x
Somma del primo = 2 · somma del secondo somma del primo = 2x
Somma del terzo = 1\3 · somma del secondo somma del terzo = 1\3 x x> 0 e x < 1640
Equazione risolvente
x + 2x + 1\3 x = 1640 moltiplicando tutti i numeri per 3 per togliere il denominatore si ottiene:
3x + 6x + x = 4920
10x = 4920 x = 4920\10 x = 492
La soluzione è accettabile
Verifica
1° membro 2° membro
492 + 2 · 492 + 1\3 · 492 = 1640
= 492 + 984 + 164 = 1640
Risposta
Il primo amico riceve 2 · 492 = 984 euro, il secondo 492 uro e il terzo 1\3 · 492 = 164 euro.
21) Un impiegato spende 2\5 del suo stipendio per il vitto, 1\3 per il muto della casa, 2\15 per l’abbigliamento e gli restano per le altre spese 240 euro. Qual è il suo stipendio mensile?
Dati Incognite
spesa vitto = 2\5 dello stipendio stipendio = x
spesa mutuo = 1\3 dello stipendio spesa vitto = 2\5 x
spesa abbigliamento = 2\15 dello stipendio spesa mutuo = 1\3x
spese varie = 240 euro spesa abbigliamento = 2\15 x
Equazione risolvente
x = 2\5 x + 1\3x + 2\15x + 240 m.c.m.(3; 5; 15) = 15
15 x = 6x + 5x + 2x + 3600
quindi 15 x – 6x – 5x – 2x = 3600
2x = 3600 x = 3600\2 = 1800 euro
22) Per l’acquisto di un’auto si sono spesi 22 000 euro, IVA compresa. Sapendo che è stato praticato uno sconto di 1040 euro e che l’IVA è del 20%, qual è il costo dell’auto senza IVA?
Dati Incognite
somma pagata = 22 000 euro costo senza IVA = x
sconto = 1040 euro
IVA = 20%
Svolgimento
L’equazione risolvente è:
x + 20\100 x – 1040 = 22 000
semplificando si ottiene:
x + 1\5 x – 1040 = 22 000
5x + x – 5200 = 110 000
5x + x = 110 000 + 5 200
6x = 115 200 x = 115200\6 = 19 200
Verifica
1° membro 2° membro
19 200 + 1\5 · 19 200 – 1040= 22 000
= 19 200 + 3 840 – 1040 = 22 000
La soluzione è accettabile, quindi il costo dell’auto senza IVA è di 19 200 euro.
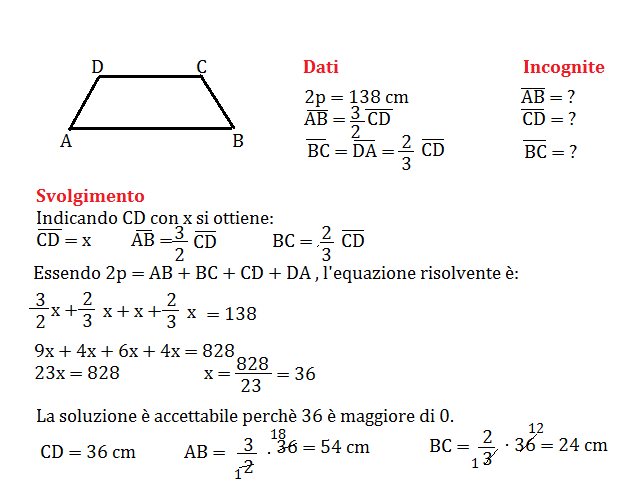
23) In un trapezio isoscele la base maggiore è 3\2 della minore e il lato obliquo è 2\3 della base minore. Calcola la lunghezza di ciascuna base e del lato obliquo sapendo che il perimetro è 138 cm.
24) In un rettangolo la base è 4\3 dell’altezza e l’area è 300 cm². Calcola le misure delle due dimensioni.
Vedi programma matematica terza media