Problemi sulla superficie del prisma retto
Problema n° 1
Un prisma triangolare retto ha per base un triangolo rettangolo avente i cateti lunghi rispettivamente 18 cm e 24 cm. Sapendo che l’altezza del prisma misura 23 cm, calcola l’area totale.
Problema n° 2
La base di un prisma retto è un triangolo isoscele avente il perimetro di 28,8 cm e la base lunga 10,8 cm. Calcola la misura dell’altezza del prisma sapendo che l’area totale è 423,36 cm².
Problema n° 3
Un prisma retto ha per base un triangolo isoscele avente la base e l’altezza lunghe rispettivamente 25 cm e 30 cm. Sapendo che l’altezza del prisma misura 18 cm, calcola l’area laterale.
Problema n° 4
Un prisma triangolare retto ha per base un triangolo rettangolo con l’ipotenusa e un cateto lunghi rispettivamente 91 cm e 84 cm. Calcola la misura dell’altezza del prisma sapendo che l’area della sua superficie laterale è 3360 cm².
Problema n° 5
L’area totale di un prisma triangolare retto è 3168 cm². Calcola la misura dell’altezza del prisma sapendo che la sua base è un triangolo rettangolo avente l’area di 504 cm² e un cateto lungo 16 cm.
Problema n° 6
Un prisma retto, alto 35 dm, ha l’area della superficie laterale di 2 100 dm². Sapendo che la base è un triangolo isoscele avente la base lunga 19,2 dm, determina l’area della superficie totale del prisma.
Problema n° 7
Le aree della superficie laterale e totale di un prisma triangolare retto sono rispettivamente 1 472 cm² e 1 712 cm². Calcola la misura dell’altezza del prisma sapendo che la base è un triangolo isoscele in cui l’altezza relativa alla base è lunga 8 cm.
Problema n° 8
Un prisma quadrangolare retto ha per base un trapezio isoscele avente le basi e l’altezza lunghe rispettivamente 58 dm, 16 dm e 28 dm. Sapendo che l’altezza del prisma misura 40 dm, calcola l’area della sua superficie totale.
Problema n° 9
Un prisma retto ha l’area della superficie totale di 2 772 cm²; sapendo che il poligono di base è un rombo con le diagonali lunghe rispettivamente 36 cm e 27 cm, determina la misura dell’altezza del prisma.
Problema n° 10
La base di un prisma retto è un trapezio rettangolo avente i lati non paralleli lunghi rispettivamente 4 dm e 5 dm e la base minore che misura 8 dm. Calcola l’area totale del prisma sapendo che la sua altezza è congruente alla base maggiore del trapezio.
Problema n° 11
La base di un prisma retto è un rombo avente la somma delle misure delle diagonali uguale a 138 cm e una di esse è 8\15 dell’altra. Calcola l’area totale del prisma sapendo che la sua altezza è congruente al lato del rombo.
Problema n° 12
La base di un prisma retto è un trapezio isoscele avente uno dei lati congruenti e la sua proiezione sulla base maggiore lunghi rispettivamente 25 cm e 7 cm. Sapendo che la base minore del trapezio è lunga 30 cm e che l’area totale del prisma è 3 078 cm², calcola la misura dell’altezza del prisma.
Problema n° 13
Un prisma pentagonale regolare ha lo spigolo di base e lo spigolo laterale lunghi rispettivamente 8 cm e 24 cm. Calcola l’area della superficie laterale e l’area della superficie totale del prisma.
Problema n° 14
Calcola le aree delle superfici laterale e totale di un prisma quadrangolare regolare avente l’area di una faccia laterale di 798 cm² e l’altezza lunga 38 cm.
Problema n° 15
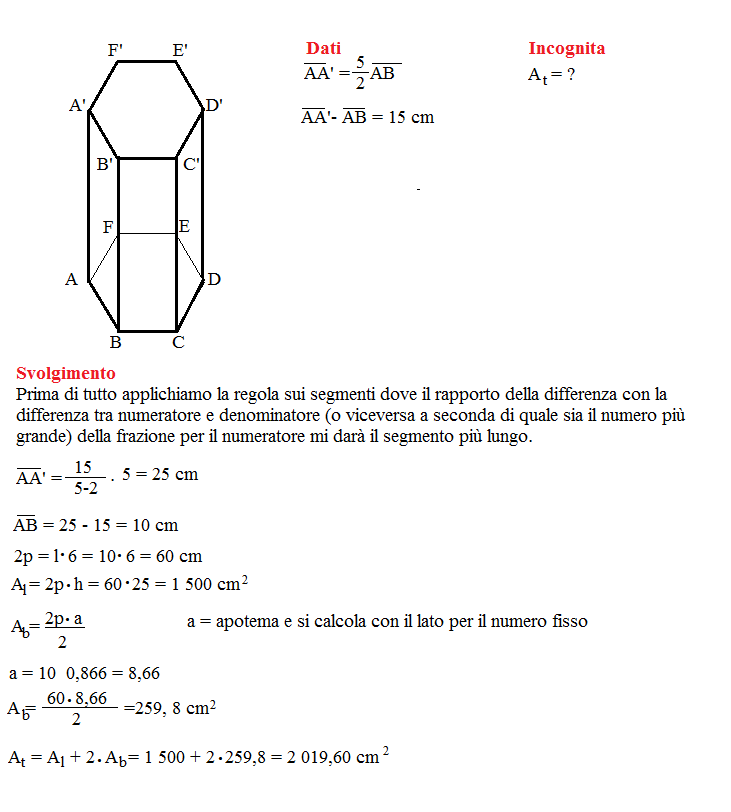
In un prisma regolare esagonale il rapporto tra lo spigolo laterale e lo spigolo di base è 5\2 e la loro differenza è 15 cm. Calcola l’area della superficie totale del prisma.
SVOLGIMENTO
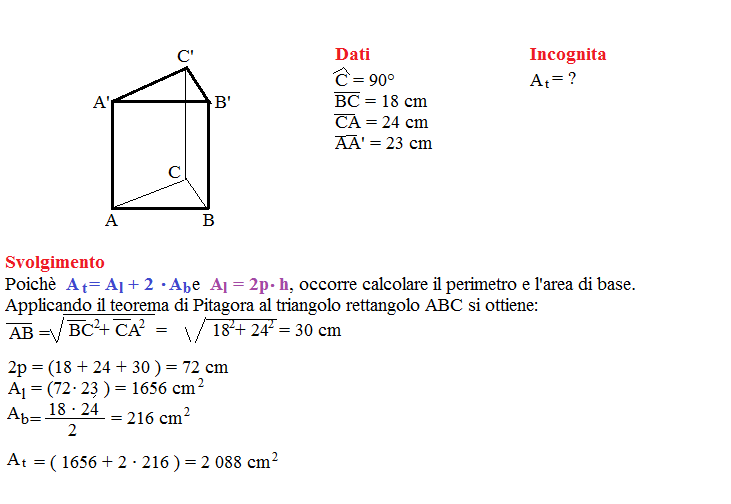
Problema n° 1
Un prisma triangolare retto ha per base un triangolo rettangolo avente i cateti lunghi rispettivamente 18 cm e 24 cm. Sapendo che l’altezza del prisma misura 23 cm, calcola l’area totale.
Problema n° 2
La base di un prisma retto è un triangolo isoscele avente il perimetro di 28,8 cm e la base lunga 10,8 cm. Calcola la misura dell’altezza del prisma sapendo che l’area totale è 423,36 cm².

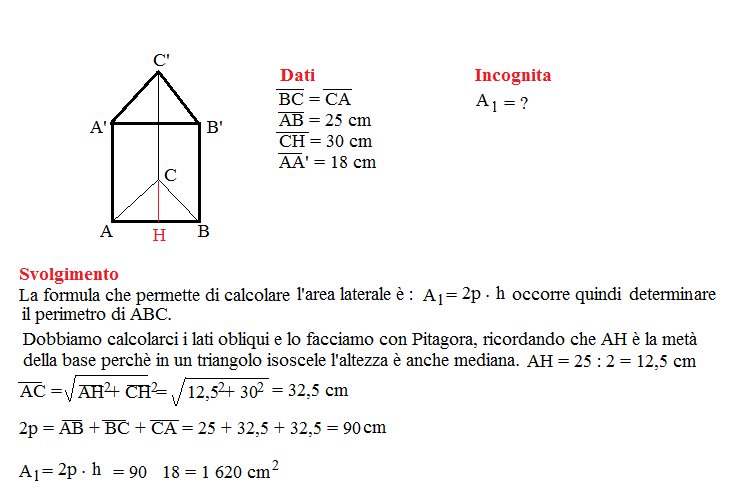
Problema n° 3
Un prisma retto ha per base un triangolo isoscele avente la base e l’altezza lunghe rispettivamente 25 cm e 30 cm. Sapendo che l’altezza del prisma misura 18 cm, calcola l’area laterale.
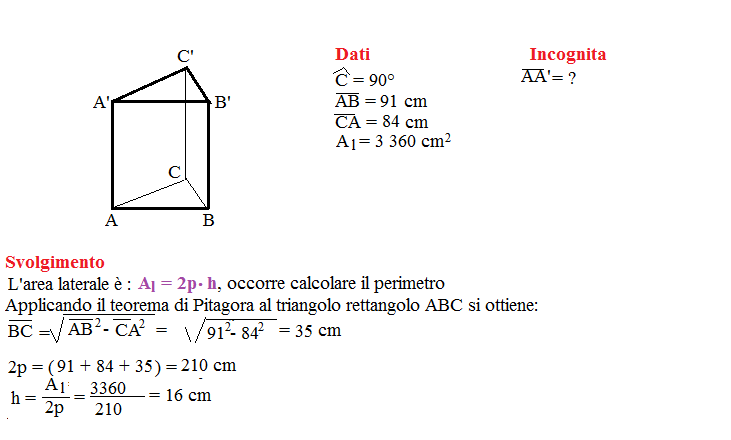
Problema n° 4
Un prisma triangolare retto ha per base un triangolo rettangolo con l’ipotenusa e un cateto lunghi rispettivamente 91 cm e 84 cm. Calcola la misura dell’altezza del prisma sapendo che l’area della sua superficie laterale è 3360 cm².
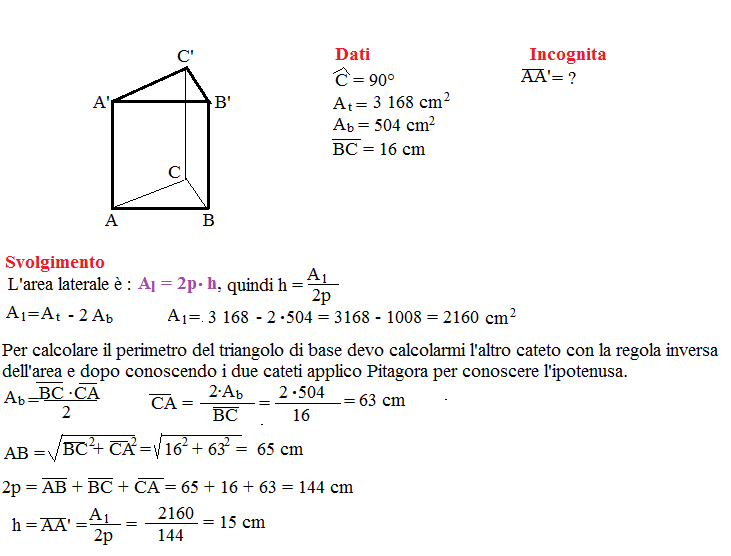
Problema n° 5
L’area totale di un prisma triangolare retto è 3168 cm². Calcola la misura dell’altezza del prisma sapendo che la sua base è un triangolo rettangolo avente l’area di 504 cm² e un cateto lungo 16 cm.
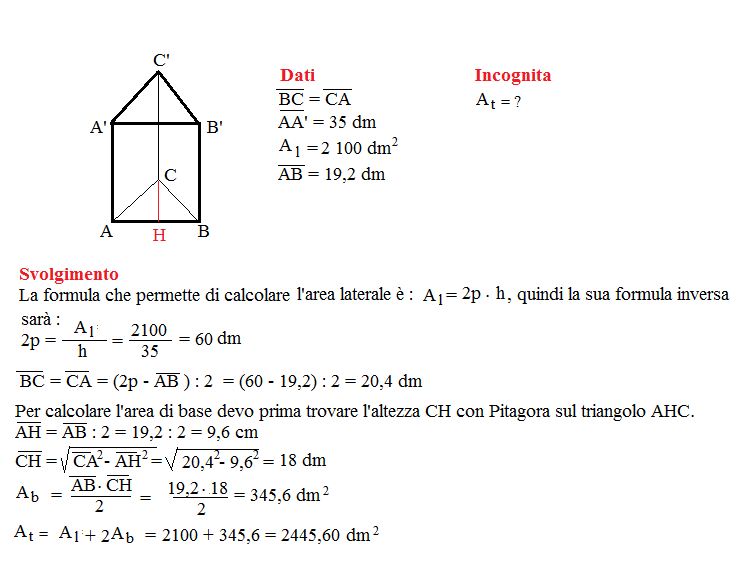
Problema n° 6
Un prisma retto, alto 35 dm, ha l’area della superficie laterale di 2 100 dm². Sapendo che la base è un triangolo isoscele avente la base lunga 19,2 dm, determina l’area della superficie totale del prisma.
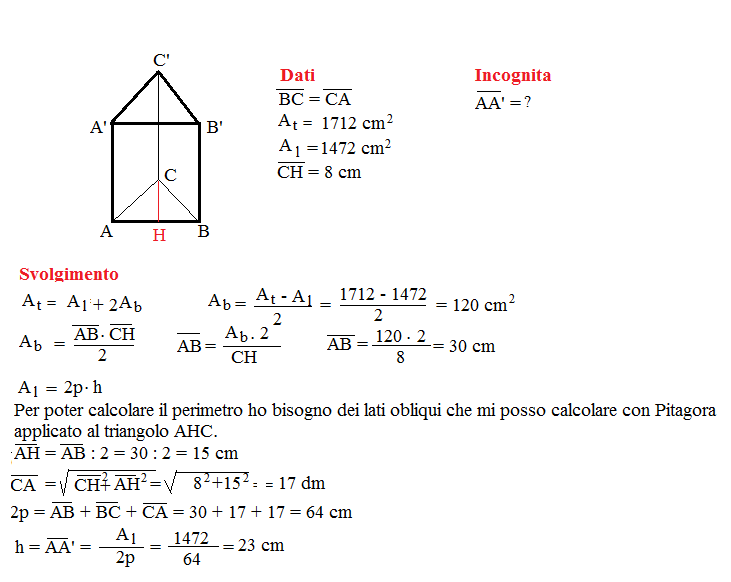
Problema n° 7
Le aree della superficie laterale e totale di un prisma triangolare retto sono rispettivamente 1 472 cm² e 1 712 cm². Calcola la misura dell’altezza del prisma sapendo che la base è un triangolo isoscele in cui l’altezza relativa alla base è lunga 8 cm.
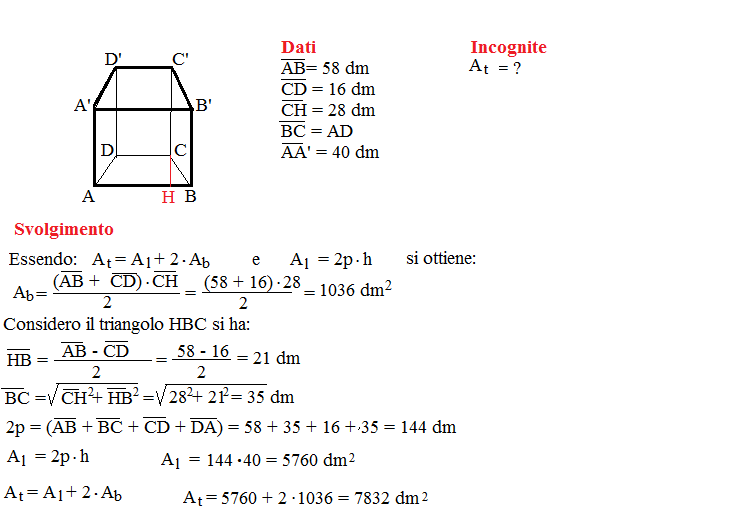
Problema n° 8
Un prisma quadrangolare retto ha per base un trapezio isoscele avente le basi e l’altezza lunghe rispettivamente 58 dm, 16 dm e 28 dm. Sapendo che l’altezza del prisma misura 40 dm, calcola l’area della sua superficie totale.
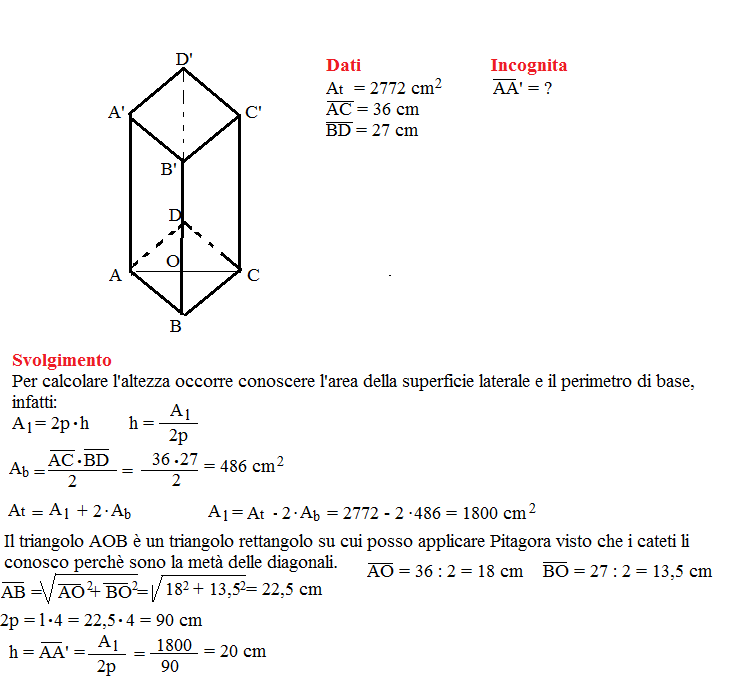
Problema n° 9
Un prisma retto ha l’area della superficie totale di 2 772 cm²; sapendo che il poligono di base è un rombo con le diagonali lunghe rispettivamente 36 cm e 27 cm, determina la misura dell’altezza del prisma.
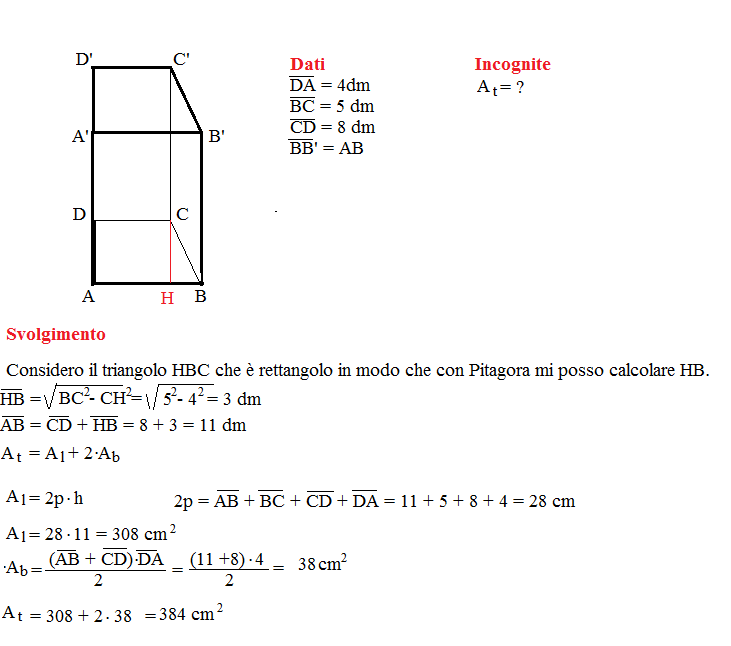
Problema n° 10
La base di un prisma retto è un trapezio rettangolo avente i lati non paralleli lunghi rispettivamente 4 dm e 5 dm e la base minore che misura 8 dm. Calcola l’area totale del prisma sapendo che la sua altezza è congruente alla base maggiore del trapezio.
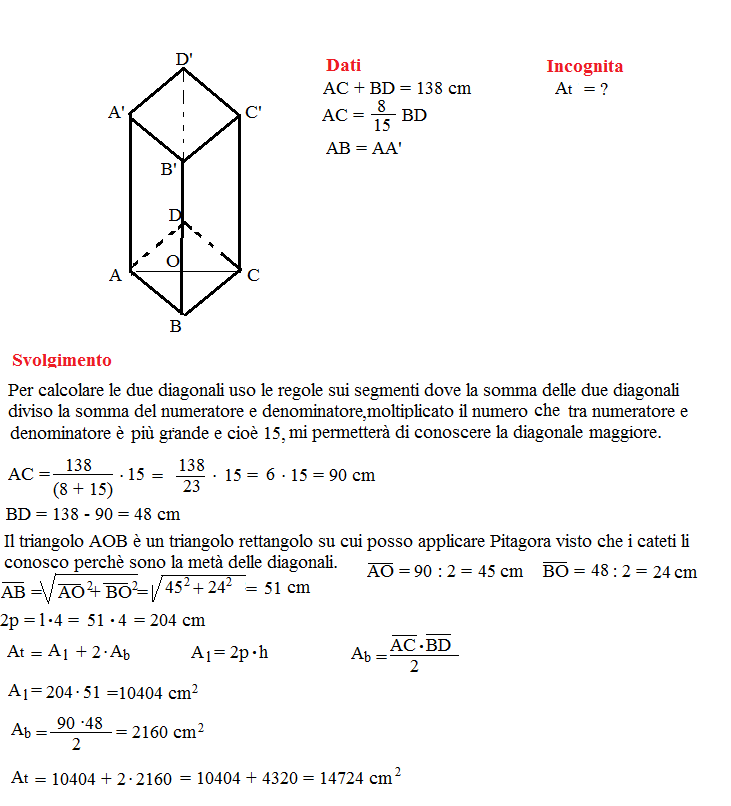
Problema n° 11
La base di un prisma retto è un rombo avente la somma delle misure delle diagonali uguale a 138 cm e una di esse è 8\15 dell’altra. Calcola l’area totale del prisma sapendo che la sua altezza è congruente al lato del rombo.
Problema n° 12
La base di un prisma retto è un trapezio isoscele avente uno dei lati congruenti e la sua proiezione sulla base maggiore lunghi rispettivamente 25 cm e 7 cm. Sapendo che la base minore del trapezio è lunga 30 cm e che l’area totale del prisma è 3 078 cm², calcola la misura dell’altezza del prisma.

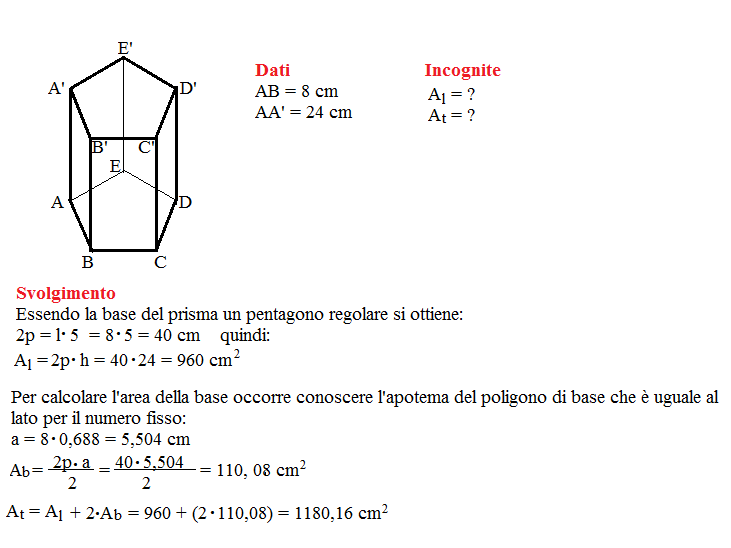
Problema n° 13
Un prisma pentagonale regolare ha lo spigolo di base e lo spigolo laterale lunghi rispettivamente 8 cm e 24 cm. Calcola l’area della superficie laterale e l’area della superficie totale del prisma.
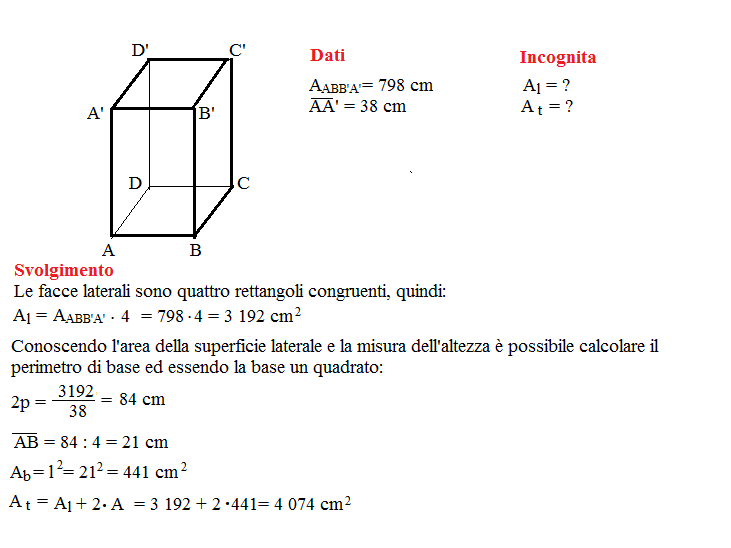
Problema n° 14
Calcola le aree delle superfici laterale e totale di un prisma quadrangolare regolare avente l’area di una faccia laterale di 798 cm² e l’altezza lunga 38 cm.
Problema n° 15
In un prisma regolare esagonale il rapporto tra lo spigolo laterale e lo spigolo di base è 5\2 e la loro differenza è 15 cm. Calcola l’area della superficie totale del prisma.