Problemi sull’area del trapezio
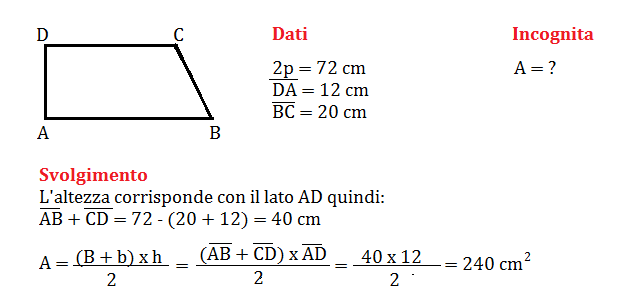
Problema n° 1
Calcola l’area di un trapezio rettangolo sapendo che il perimetro è 72 cm e che l’altezza e il lato obliquo misurano rispettivamente 12 cm e 20 cm.
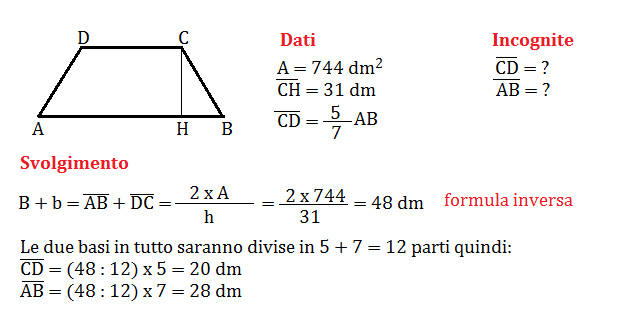
Problema n° 2
Un trapezio ha l’area di 744 dm² e l’altezza misura 31 dm. Calcola le lunghezze delle due basi sapendo che la minore è della maggiore.
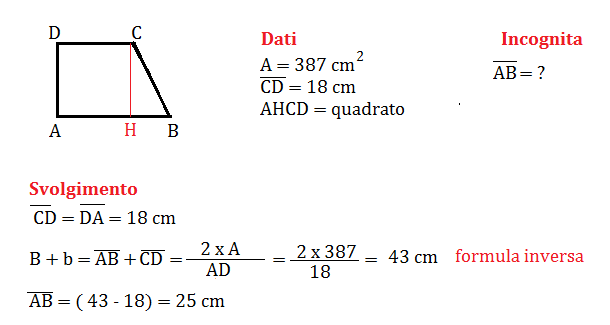
Problema n° 3
Un trapezio rettangolo è formato da un quadrato e da un triangolo rettangolo avente un cateto coincidente con uno dei lati del quadrato. Sapendo che l’area del trapezio è 387 cm² e che la sua base minore è lunga 18 cm, calcola la misura della base maggiore.
Problema n°4
Un trapezio isoscele ha le basi lunghe rispettivamente 28 cm e 15 cm. Calcola l’area del trapezio sapendo che gli angoli adiacenti alla base maggiore misurano 45° ciascuno.
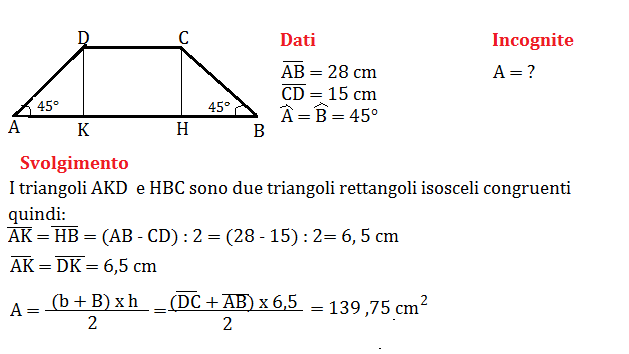
Problema n° 5
Calcola l’area di un trapezio che ha le basi lunghe 35 cm e 21 cm e i lati obliqui che misurano rispettivamente 15 cm e 13 cm.

Problema n° 6
Calcola l’area di un trapezio rettangolo sapendo che il lato obliquo misura 24 cm, l’altezza è i 2\3 del lato obliquo e il perimetro misura 70 cm.
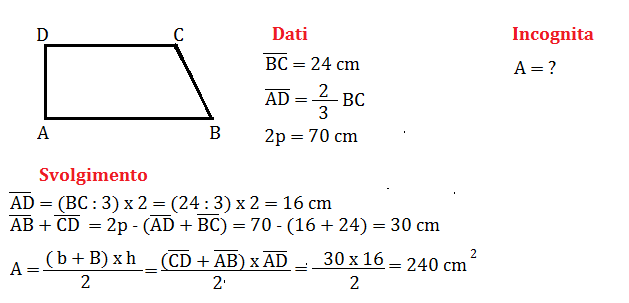
Problema n° 7
L’area di un trapezio rettangolo, avente la base minore uguale all’altezza e pari alla metà della base maggiore, misura 96 cm². Calcola la misura delle basi e dell’altezza del trapezio.
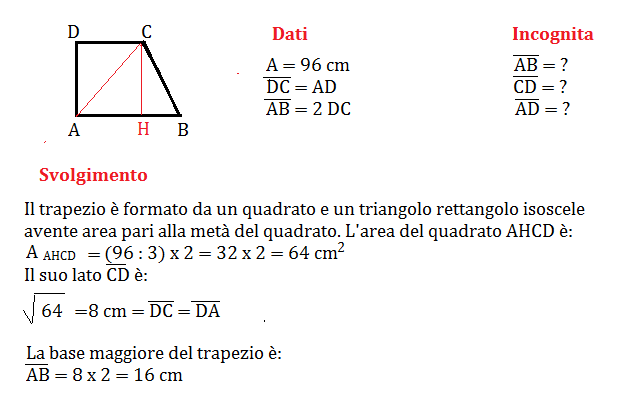
Problema n° 8
Determina la misura delle proiezioni dei lati obliqui di un trapezio isoscele sulla base maggiore sapendo che l’area misura 480 dm², l’altezza 16 dm e che una base è i 3\7 dell’altra.
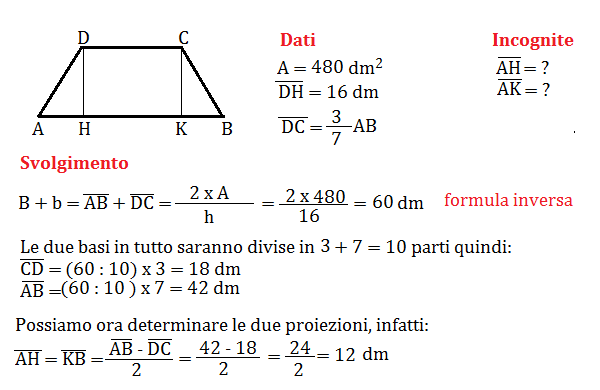
Problema n° 9
Il lato obliquo di un trapezio rettangolo che ha l’angolo acuto di 60° misura 11,56 m e l’altezza, che è uguale alla base minore, misura 10 m. Calcola la sua area.

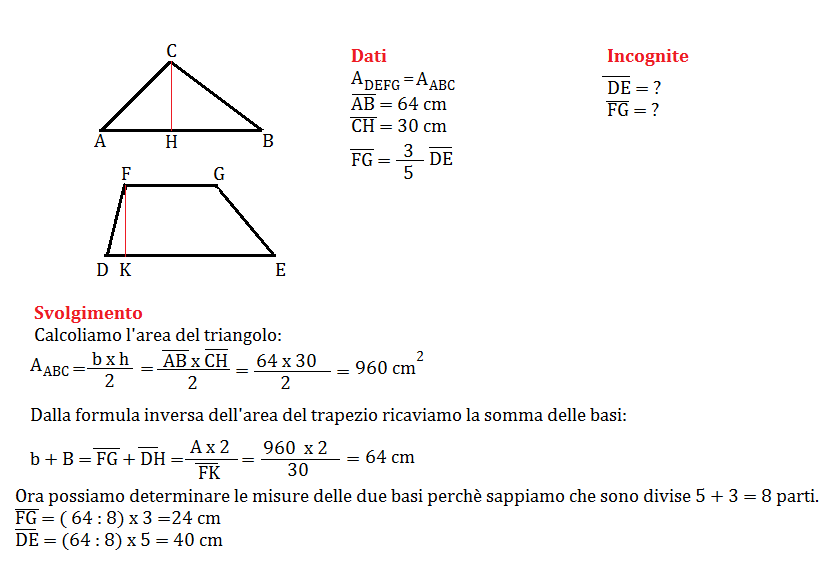
Problema n° 10
Un trapezio è equivalente a un triangolo avente le basi pari a 64 cm e l’altezza di 30 cm. Calcola la misura delle basi del trapezio sapendo che sono una i 3\5 dell’altra, e che l’altezza del trapezio è uguale all’altezza del triangolo.