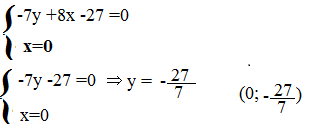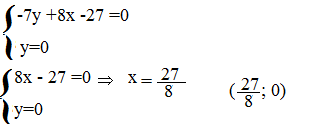ESERCIZIO N° 1
Scrivi l’equazione della retta che è perpendicolare alla retta passante per A(-2;-5) e B(3; 1) e che passa per il punto C(2;-3).
ESERCIZIO N° 2
Fra le rette parallele alla retta r di equazione x +2y – 10=0 determina quella che passa per il punto P(4;-3).
ESERCIZIO N° 3
Scrivi l’equazione della retta passante per i punti A(-2; -2) e B(6; 10). Determina su tale retta un punto C la cui ascissa è la metà dell’ordinata.
ESERCIZIO N° 4
Fra le rette perpendicolari alla retta s di equazione 3x – 6y + 1 = 0 determina:
a)la retta a che passa per il punto A(1,3);
b)la retta b che passa per l’origine.
ESERCIZIO N° 5
Fra le rette passanti per il punto P(1; 3) determina:
a)l’equazione della retta che interseca l’asse x nel punto A(2; 0);
b)l’equazione della retta che interseca l’asse y nel punto B(0; -1).
ESERCIZIO N° 6
I punti A(-3; 1), B(6; 3) e C(-1; -5) sono i vertici di un triangolo. Determina:
a)le equazioni delle rette contenenti i tre lati;
b)le coordinate dei punti d’intersezione della retta contenente BC con gli assi cartesiani.
SVOLGIMENTO
ESERCIZIO N° 1
Scrivi l’equazione della retta che è perpendicolare alla retta passante per A(-2;-5) e B(3; 1) e che passa per il punto C(2;-3).
La retta passante per AB la calcolo con la retta passante per due punti
quindi otteniamo:
5(y+5) =6(x +2) ⇒ 5y + 25 = 6x + 12 ⇒ 5y = 6x + 12 – 25 ⇒ y = 6\5x – 13\5
Il coefficiente angolare è m=6\5
La retta perpendicolare avrà coefficiente angolare m’= – 1\m ⇒ m’= -5\6 e passerà per C(2; -3)
⇒ y +3 = -5\6(x – 2) ⇒ y + 3 = -5\6x + 5\3
y= -5\5x + 5\3 – 3 ⇒ y= -5\6x -4\3 ⇒ 6y = -5x – 8 ⇒ 6y +5x +8 = 0
ESERCIZIO N° 2
Fra le rette parallele alla retta r di equazione x +2y – 10=0 determina quella che passa per il punto P(4;-3).
x + 2y – 10 = 0 il cui coefficiente angolare è m= -a\b = -1\2
⇒ y + 3 = -1\2(x – 4) quindi
facciamo il minimo comune multiplo
ESERCIZIO N° 3
Scrivi l’equazione della retta passante per i punti A(-2; -2) e B(6; 10). Determina su tale retta un punto C la cui ascissa è la metà dell’ordinata.
Uso la formula della retta passante per i due punti.
8(y + 2) = 12(x + 2) ⇒ 8y + 16 = 12x + 24 ⇒ 8y – 12x -8 =0 divido tutto per -4 e ottengo:
3x – 2y + 2 =0
chiamiamo z l’ordinata del punto C e z\2 l’ascissa.
Sostituisco queste coordinate nell’equazione trovata.
3(z\2) – 2(z) + 2 =0 ⇒ -1\2z = – 2 ⇒ z = 4 quindi le coordinate di C sono (2; 4)
ESERCIZIO N° 4
Fra le rette perpendicolari alla retta s di equazione 3x – 6y + 1 = 0 determina:
Il coefficiente angolare della retta è m= – a\b = 3\6 = 1\2
a)la retta a che passa per il punto A(1,3);
il suo coefficiente angolare sarà -1\m quindi = 2
⇒ y – 3 = -2(x – 1) ⇒ y = -2x + 2 + 3 ⇒ y = -2x + 5
b)la retta b che passa per l’origine.
il suo coefficiente essendo anch’essa perpendicolare alla retta data è 2, il punto attraverso cui passa è O(0,0). Avremo:
⇒ y – 0 = – 2 (x – 0) ⇒ y = -2x
ESERCIZIO N° 5
Fra le rette passanti per il punto P(1; 3) determina:
a)l’equazione della retta che interseca l’asse x nel punto A(2; 0);
b)l’equazione della retta che interseca l’asse y nel punto B(0; -1).
Prima di tutto consideriamo il fascio passante per P lasciando m come incognita.
⇒ y – 3 = m(x -1)
a)tale fascio passa anche per il punto A quindi andiamo a sostituire le sue coordinate a x ed a y. Avremo:
0 – 3 = m(2-1) quindi m = -3
La retta che cerchiamo sarà ⇒ y – 3 = m(x -1), però questa volta conosciamo m quindi sarà:
y – 3= -3(x – 1) ⇒ y – 3 = -3x + 3 ⇒ y = -3x + 6
b)tale fascio passa anche per il punto B quindi andiamo a sostituire le sue coordinate a x ed a y. Avremo:
partendo da y – 3 = m(x -1) otteniamo 1 – 3 = m (0-1) ⇒ m = 4
Conoscendo il valore di m lo andiamo a sostituire in y – 3 = m(x -1) e otteniamo y – 3 = 4(x – 1) ⇒ y – 3 = 4x – 4 ⇒
y = 4x – 1
ESERCIZIO N° 6
I punti A(-3; 1), B(6; 3) e C(-1; -5) sono i vertici di un triangolo. Determina:
a)le equazioni delle rette contenenti i tre lati;
⇒ 9y – 9 = 2x + 6 ⇒ -9y + 2x + 15 =0
⇒ 2y -2= -6x – 9 ⇒ 2y +6x + 7⇒ y + 3x + 7\2=0
7y -21 = 8x – 48⇒ 7y -8x + 27=0
b)le coordinate dei punti d’intersezione della retta contenente BC con gli assi cartesiani.
Intersezione con l’asse y quindi con x=0
Intersezione con l’asse x quindi con y=0
Programma di matematica secondo superiore
Programma matematica terzo superiore