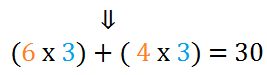Proprietà delle operazioni
Conoscere le proprietà delle operazioni ti permette di eseguire i calcoli in modo più veloce.
Proprietà dell’addizione
PROPRIETA’ COMMUTATIVA
Cambiando l’ordine degli addendi il risultato non cambia. Questa proprietà si applica per eseguire la prova dell’addizione
a+b=b+a
13+4+9=26 9+13+4 =26
PROPRIETA’ ASSOCIATIVA
La somma di tre o più addendi non cambia se a due o più di essi si sostituisce la loro somma.
a+b+c=(a+b)+c=a+(b+c)
64+37+13=114 (64+37)+13=101+13=114 64+(37+13)=64+50=114
PROPRIETA’ DISSOCIATIVA
La somma di più addendi non cambia se a un addendo ne sostituiscono altri aventi per somma l’addendo sostituito.
a+b= (c+d)+b
34+49=83 34+(40+9)=34+40+9=74+9=83
LO ZERO E’ L’ELEMENTO NEUTRO DELL’ADDIZIONE
12+0=12
Proprietà della sottrazione
Proprietà della sottrazione
PROPRIETA’ INVARIANTIVA
Aggiungendo o togliendo uno stesso numero sia al minuendo che al sottraendo di una sottrazione il risultato non cambia.
ESEMPI:
28 – 8=20 ; 27 – 14=13
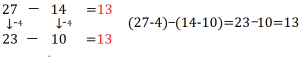
Proprietà della moltiplicazione
PROPRIETA’ COMMUTATIVA
Cambiando l’ordine dei fattori il prodotto non cambia. Questa proprietà si applica per eseguire la prova.
a x b= b x a
2 x 14 x 5 = 140 14 x 5 x 2 =140
(+4) x (-2)= (-2) x (+4)
PROPRIETA’ ASSOCIATIVA
Se sostituisci a due fattori il loro prodotto il risultato non cambia.
a x b x c = (a x b) x c= a x (b x c )
6 x 4 x 25 =600 (6 x 4) x 25= 24 x 25 = 600
PROPRIETA’ DISTRIBUTIVA
Per moltiplicare una somma o una differenza per un numero si può moltiplicare per quel numero ciascun termine della somma o differenza e poi addizionare o sottrarre i prodotti ottenuti.
(a+b) x c= (a x c) + (b x c)
PROPRIETA’ DISSOCIATIVA
Il prodotto di più fattori non cambia se a un fattore ne sostituiscono altri aventi per prodotto il fattore sostituito.
a x b=(c x d) x b 25 x 12=300 25 x (3 x 4)= 300
La prova della moltiplicazione si ottiene cambiando l’ordine dei fattori e se il risultato è uguale allora non si sono commessi errori.
Proprietà della divisione
PROPRIETA’ INVARIANTIVA
Moltiplicando o dividendo, per uno stesso numero diverso da zero entrambi i termini di una divisione il quoziente non cambia e il resto se c’è, rimane moltiplicato o diviso per quello stesso numero.
a : b = ( a x c) : ( b x c ) o a: b = ( a:c) : (b: c)
18 : 6 = 3 (18 x 5 ) : ( 6 x 5) = 90 : 15= 3
Se la divisione è impropria quindi prevede un resto, anche esso risulterà moltiplicato o diviso per il numero usato .
Per i numeri decimali tale proprietà si applicherà moltiplicando per 10,100,1000… per eliminare la virgola del divisore.
585,6 : 7,32 = (585,6 x 100) : ( 7,32 x 100) = 58560 : 732 = 80
PROPRIETA’ DISTRIBUTIVA
Per dividere una somma ( o una differenza) indicata per un numero, basta dividere ciascun termine per quel numero e addizionare o sottrarre i quozienti ottenuti .
(a + b ) : c = (a : c ) + ( b : c ) (a – b ) : c = (a : c) – (b : c)
( 36 + 48 ) : 12 = 84 : 12 = 7 ⇒ ( 36: 12 ) + ( 48 : 12 ) = 3 + 4 = 7
Questa proprietà si può applicare solo se la somma o la differenza sono dividendi e cioè sono i primi termini della divisione, infatti se è il contrario il risultato sarà diverso quindi non sarà possibile applicare tale proprietà.
72 : ( 6 + 3 ) = 79 : 9 ≠ 72 : ( 6 + 3 ) = 72 : 6 + 72: 3 = 12 + 24 = 36