I grafici che permettono di visualizzare meglio le percentuali sono gli areogrammi. L’ areogramma più usato per rappresentare la % è quello a settori circolari detto areogramma percentuale.
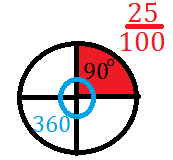
Consideriamo un cerchio e dividiamolo in 4 parti quindi avremo un settore circolare pari a 1\4 poichè 1\4=25\100, quindi possiamo dire che la parte colorata è il 25% dell’intero cerchio.
L’ampiezza del settore circolare è 90° che è 1\4 dell’angolo al centro che è uguale a 360°.
Infatti 1\4 = 90\360
I due rapporti 25\100 e 90\360 sono uguali dunque possiamo scrivere la proporzione : 25: 100= 90° : 360°.
Le due grandezza, superficie del settore circolare e ampiezza del settore circolare sono direttamente proporzionali pertanto il problema della costruzione di un areogramma a settori circolari è riconducibile a un problema del tre semplice: le grandezze sono il tasso % r e l’ampiezza dell’angolo al centro α.
r: 100 = α : 360°
PROBLEMA
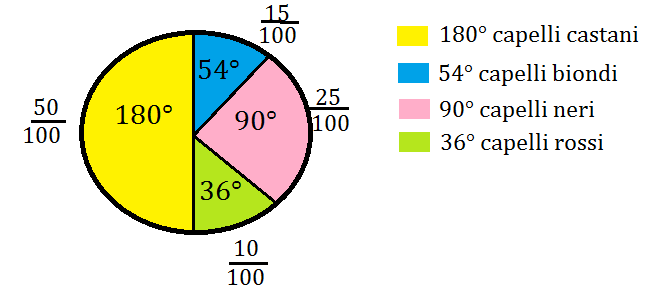
In una classe il 15 % degli alunni ha i capelli biondi, il 25% ha i capelli neri, il 10% ha i capelli rossi e il 50%, ha i capelli castani. Rappresenta la % con un areogramma.
Indicando con x, y ,z e t l’ampiezza dei settori corrispondenti alle percentuali si ha:
15 : 100= x : 360° da cui x= 54 °
25 : 100 =y : 360° da cui y= 90°
10: 100= z: 360° da cui z= 36°
50:100= t : 360° da cui t= 180°
Rappresentiamoli sull’aerogramma e otteniamo: