RETTE PARALLELE ALL’ASSE X
Le rette parallele all’asse x sono caratterizzate dall’avere tutti i punti con coordinate (x,b) dove b è una costante, un numero fisso, che indica la posizione della retta rispetto all’asse x, mentre x varia e può essere un numero reale qualsiasi.
Questo significa che se due punti hanno la stessa ordinata b, allora appartengono ad una stessa retta parallela all’asse delle ascisse.
ESEMPIO
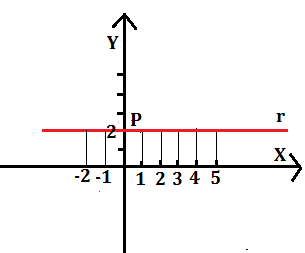
Consideriamo una retta r parallela all’asse x che incontra l’asse y nel punto P di ordinata +2.Poichè tutti i punti di r hanno uguale distanza dall’asse x, cioè hanno l’ordinata y=+2, diciamo che y=2 è l’equazione della retta parallela all’asse x.
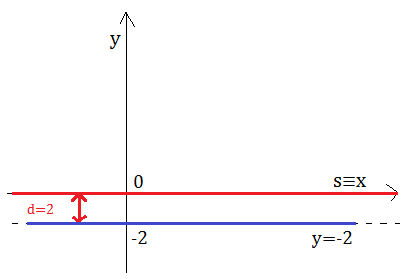
Sia s una retta che coincide con l’asse x. La sua distanza dall’asse x è zero e la sua equazione y=0
L’equazione di una retta parallela all’asse x è del tipo y = k dove k indica l’ordinata di tutti i punti della retta:
- se k > 0 la retta giace nel I e nel II quadrante;
- se k < 0 la retta giace nel III e IV quadrante;
- se k = 0 la retta coincide con l’asse x e y = 0 è l’equazione dell’asse x.
Esercizio
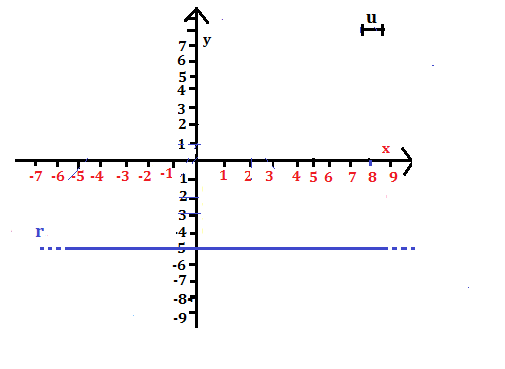
Con riferimento alla figura, esegui quanto indicato.
a) Scrivi le coordinate di tre punti A,B,C, appartenenti alla retta r e aventi le ascisse rispettivamente uguali a -3; +1; +5.
Tutti i punti della retta r hanno l’ordinata uguale a – 5, quindi i punti sono:
A (-3; -5), B (+1; -5), C (+5; -5)
b) Scrivi l’equazione della retta r. L’Equazione della retta r è: y = -5
c) Indica i quadranti su cui giace la retta r. La retta r giace sul III e IV quadrante.
d) Indica la distanza tra la retta r e l’asse x.
La distanza è : d= = 5 u
Programma matematica terza media
Programma matematica secondo superiore
Programma matematica terzo superiore