RETTE PARALLELE TRA LORO
Sappiamo che il coefficiente angolare indica la pendenza di una retta rispetto all’asse x . Quindi due rette parallele , avendo rispetto ad x la stesa pendenza , avranno anche lo stesso coefficiente angolare
Le rette parallele hanno equazione del tipo:
y=mx+ parallela a y=mx+
Quindi hanno un diverso termine noto ma lo stesso coefficiente angolare.
Sono parallele ad esempio:
y=1\2x+1; y=1\2x; y=1\2x -15. hanno tutte lo stesso coefficiente angolare.
Possiamo anche dire che due rette che hanno lo stesso coefficiente angolare allora sono parallele.
L’equazione y=a con a∈R individua una retta parallela all’asse x;
L’equazione x=b con b∈R individua una retta parallela all’asse y.
Esercizio
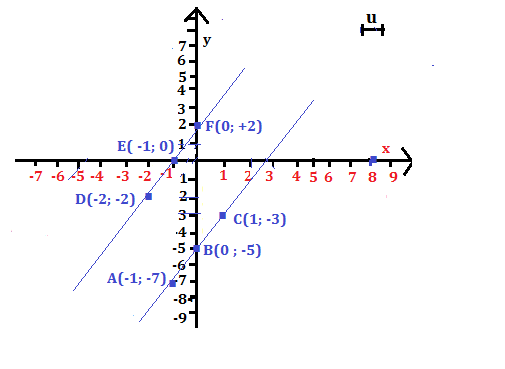
Rappresenta in un sistema di assi cartesiani la retta di equazione y = +2x – 5 e la retta a essa parallela e passante per il punto P (0; +2). Qual è la sua equazione?
La retta y = +2x – 5 ha coefficiente angolare m = +2 e quindi la retta ad essa parallela avrà coefficiente angolare uguale quindi m= +2.
Visto che la seconda retta dovrà passare per il punto P, sostituiamo tutti i dati conosciuti nell’equazione y = mx + q.
+2 = +2 (0) + q ⇒ q = +2
L’equazione della retta sarà y = 2x + 2
La tabella dei valori per y = +2x – 5 sarà:
| x | -1 | 0 | 1 |
| y | -7 | -5 | -3 |
Quindi la retta passera per i punti A (-1; -7), B (0; -5), C ( 1; -3).
La tabella dei valori per y = 2x + 2 sarà:
| x | -2 | -1 | 0 |
| y | -2 | 0 | +2 |
Quindi la retta passera per i punti D( – 2 ; -2), E (-1 ; 0), F (0 ; +2)