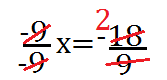Per risolvere un’equazione possiamo dire che:
- Si libera l’equazione dei denominatori, se ve ne sono, moltiplicando tutti i termini per il loro minimo comune multiplo;
- Si tolgono le parentesi, se ve ne sono, eseguendo le operazioni indicate;
- Si trasportano nel primo membro tutti i termini che contengono l’incognita e nel secondo membro tutti i termini noto;
- Si riducono, in entrambi i membri, i termini simili;
- Si dividono i due membri per il coefficiente dell’incognita, se è diverso da zero.
Il quoto che compare al secondo membro è la radice dell’equazione.
Esempi:
1)
facciamo il minimo comune multiplo che è 12;
si moltiplicano entrambi i membri per 12 in modo da eliminare il denominatore dopo aver svolto le parentesi
3(x+1)-4(2x+5)=4x+41
3x+3-8x+20=4x+41
Si trasportano i termini con l’incognita al primo membro e quelli senza l’incognita al secondo membro e quindi ricordandoci di cambiare di segno ogni volta che ci si sposta da un membro all’altro si ha:
3x-8x-4x=-3-20+41 a questo punto si riducono i termini simili e quindi si svolgono delle somme algebriche;
-9x= +18 dividendo entrambi i membri dell’equazione per -9 si ha:
x=-2 che è la radice dell’equazione che è determinata
2) 5x-3(x-1)=2x+7 si ha:
5x-3x+3=2x+7 ⇒ 5x-3x-2x=-3+7
0·x=+4 ⇒ 0= 4 l’equazione è impossibile, perchè, 0 non può essere uguale a 4
3) 2(x+3)-4x=6-2x si ha:
2x+6-4x=6-2x ⇒2x+2x-4x=-6+6
0·x=0 ⇒ 0=0 l’equazione è indeterminata