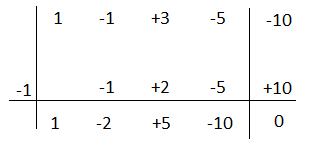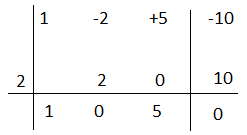Scomposizione con Ruffini
Il teorema di Ruffini permette di scomporre in fattori un polinomio. Infatti sappiamo che se un polinomio A(x) assume il valore 0 quando a x si sostituisce un valore a, allora il polinomio è divisibile per x -a.
Effettuando la divisione A(x): (x-a), otteniamo il polinomio quoziente Q(x) e , poichè il resto è zero, scriviamo A(x) come prodotto di due fattori: A(x) =(x-a)Q(x).
Quindi dobbiamo trovare un valore a in modo che sostituito al polinomio mi dia come risultato 0.
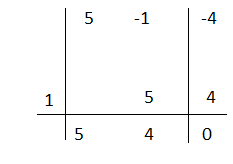
Per esempio consideriamo il polinomio 5x² – x – 4, tentiamo con 1 e lo sostituiamo alla x e abbiamo:
A(1)= 5(1)² – (1) – 4 = 5 – 1 – 4 = 0 ; quindi il polinomio è divisibile per x-1. A questo punto possiamo applicare la regola di Ruffini.
Q(x)=5x+4 pertanto 5x² – x – 4= (x-1)(5x+4)
Esempio
– x³ + 3x² – 5x – 10
Esso si annulla per x = -1 e per x=2. Infatti:
P(-1)= – (-1)³ + 3(-1)²- 5(-1) – 10= 1 + 1 + 3 + 5 – 10 = 0 Infatti applichiamo prima Ruffini per x=-1.
Q(x)= – 2x² +5x – 10 possiamo ancora scomporlo e vediamo che si annulla per x=2 quindi applichiamo nuovamente Ruffini.
Q(x)= x² + 5
La scomposizione finale sarà:
– x³ + 3x² – 5x – 10= (x-1)(x+2)( x² + 5)