SIMMETRIA RISPETTO AD UNA RETTA

LA SIMMETRIA ASSIALE COME CORRISPONDENZA BIUNIVOCA
Abbiamo detto che due punti si dicono simmetrici rispetto ad una retta se hanno uguale distanza dalla retta.
Assegnando perciò una retta r possiamo costruire di un qualsiasi punto A il suo simmetrico A’. Al punto A possiamo quindi far corrispondere il punto A’. Viceversa, se assegniamo il punto A’, possiamo ad esso far corrispondere il punto A.

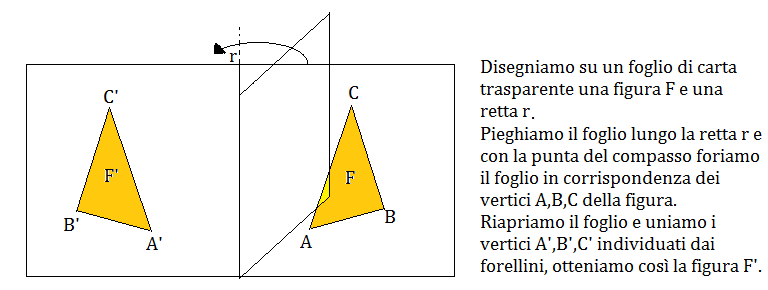
La simmetria assiale è un ribaltamento, infatti, per ottenere F’ abbiamo effettuato un movimento che ha fatto uscire F dal piano su cui giace. Se ricalchiamo la figura F su un foglio di carta trasparente e proviamo a spostare il foglio sul piano in modo da far sovrapporre F a F’ ci accorgiamo che ciò non è possibile: occorre proprio effettuare un movimento che faccia uscire F dal piano.
Le due figure F ed F’, per come sono state ottenute, sono congruenti:
I vertici A,B,C di F si susseguono in verso antiorario mentre i vertici A’,B’,C’ di F’ si susseguono in verso orario: la simmetria assiale è un’isometria inversa; F ed F’ sono inversamente isometriche.
