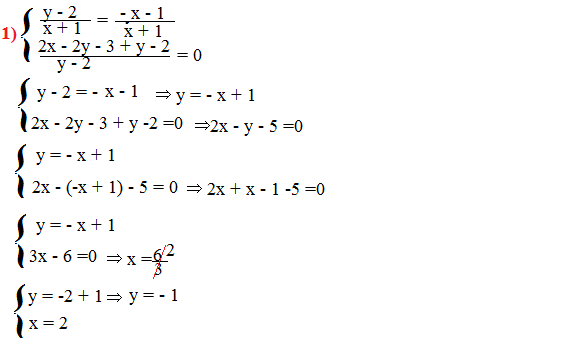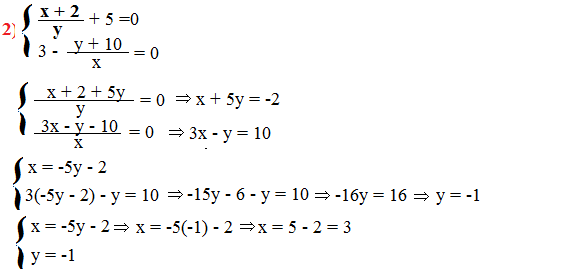Un sistema lineare è fratto se ha almeno una equazione fratta cioè con l’incognita al denominatore.
Un sistema lineare fratto, quando si riduce in forma normale diventa un sistema lineare intero, però per poter eliminare i denominatori è necessario stabilire le condizioni di esistenza, cioè trovare quei valori che rendono nullo il denominatore e che quindi non possono essere soluzioni del sistema.
Una volta effettuato il sistema e trovata la soluzione, bisogna verificare che questa soluzione sia compatibile con la condizione di esistenza.
Consideriamo degli esempi per meglio capire ciò che è stato detto fino ad ora.
Le due equazioni fratte hanno senso solo se x + 1≠0 e y -2 ≠ 0. Quindi la condizione di esistenza è la seguente:
C.E. : x≠-1 ∧ y ≠2
A questo punto dobbiamo rendere il sistema in forma normale, quindi dobbiamo dare il minimo comune multiplo.
La soluzione del sistema è (2; -1)
L a condizione di esistenza è y≠ 0 e x ≠ 0.
A questo punto si riduce il sistema in forma normale e si eliminano i denominatori. Applicheremo poi il metodo della sostituzione.
La soluzione del sistema è (3; -1)