I sistemi di disequazioni sono un insieme di più disequazioni nella stessa incognita, per le quali cerchiamo le soluzioni comuni.
Le soluzioni non sono altro che quei numeri reali che contemporaneamente soddisfano entrambe le disequazioni.
Vediamo un esempio , così poi i successivi cercate d farli voi, ovviamente vi metterò sempre lo svolgimento così da poter verificare se il procedimento usato sia quello giusto.
Esempio
Risolviamo separatamente le due disequazioni:
1) Considero la sua equazione associata
x² + 2x – 15 =0 Trovo il valore della x
Δ=b²- 4ac = 4+60=64 x =
Δ >0 la disequazione è ≤ 0 allora avremo soluzioni interne, quindi -5≤x≤3
2) x² – 7x +8x -20 ≥0 ⇒ x² + x – 20 ≥0
Aquesto punto mi calcolo il delta e vedo quanto vale la x.
Δ=b²- 4ac =1 + 80 = 81
x= =
Δ >0 la disequazione è ≥ 0 quindi le soluzioni saranno esterne x≤5 e x≥4.
A questo punto portiamo le soluzioni sul grafico, le oluzioni d ogni disequazione andranno su una linea e la soluzione finale sarà quella dove ci sono solo linee continue.
Da come vediamo in questo sistema non ci sono linee continue negli stessi intervalli, quindi non ci sono soluzioni ma visto che per entrambe le disequazioni la x = -5 , questa è una soluzione.
Esercizi
Svolgi i seguenti sistemi di disequazione.
n°1
n°2
n°3
n°4
SVOLGIMENTO
n°1
Svolgiamole separatamente le due disequazioni:
- x² – 4≥ 0 consideriamo l’ equazione associata , x² -4 =0
x = visto che la disequazione è minore di zero allora le soluzioni saranno interne -2 ≤x≤2
- x(x+4)<0, considero l’equazione associata quindi x(x+4)=0
Quindi x=0 e x+4=0 ⇒ x=-4 , la disequazione è negativa quindi le soluzioni saranno interne -4<x<0
Portiamo le soluzioni sul grafico:
La soluzione del sistema è -2 ≤x≤2
n°2
Svolgiamo separatamente le due disequazioni:
- 6x² -5x + 1 ≥0 l’equazione associata è 6x² -5x + 1=0
Δ=b²- 4ac = 25-24 =1
quindi :
;
Delta maggiore di zero, disequazione maggiore di zero, le soluzioni saranno esterne, quindi: x ≤ e x ≥
quindi l’equazione associata è
Δ=b²- 4ac =3 – 8 = -5 quindi Δ<0, disequazione minore di zero, non ci sono soluzioni, quindi sul grafico sarà tutta una linea tratteggiata. Per questo motivo il sistema è inutile disegnarlo perchè non ci potranno mai essere intervalli non tutte linee continue. Il sistema è impossibile.
n°3
Svolgiamo separatamente le due disequazioni:
A questo punto per la disequazione dacciamo la regola dei segni, quindi poniamo il numeratore e il denominatore maggiore di zero.
- x² -3x + 5 ≥0 questa disequazione ha il Δ=b²- 4ac =9 -20 = -11 quindi Δ<0 disequazione >0 le soluzioni saeano tutte quelle reali quindi :
- x + 2 >0 ; x – 3> 0 le soluzioni saranno x>-2 e x>3.
Portiamo entrambe le soluzioni sul grafico e facciamo la regola dei segni e prendiamo le soluzioni negative, visto che la disequazine di partenza è negativa.
x -19 ≤ 0 ⇒ x ≤19
Portiamo i risultati sul sistema.
n°4
Svolgiamo separatamente le tre disequazioni:
- x²+4x +4≥0 Δ=b²- 4ac = 16 -16 =0 quindi:
Quindi Δ=0 disequazione ≥0 quindi la soluzione è:
- quindi x²>0 con x≠0
- essendo una disequazione fratta facciamo la regola dei segni:
2x² +2x+1> 0 considero l’equazione associata 2x² +2x+1= 0 Δ=b²- 4ac = 4-4 =0 e quindi
Visto che Δ=0 e la disequazione >0 la soluzione è:
In questo caso è inutile metterre sul grafico le soluzioni perchè sono tutte linee continue quindi la soluzione è:
Programma matematica terzo superiore

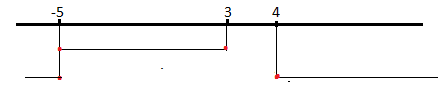
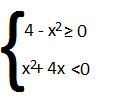
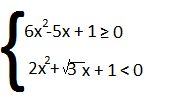
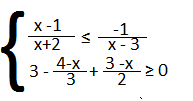
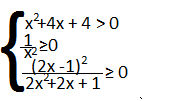


 La soluzione è -2<x<3
La soluzione è -2<x<3 Il risultato è -2<x<3
Il risultato è -2<x<3