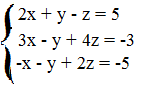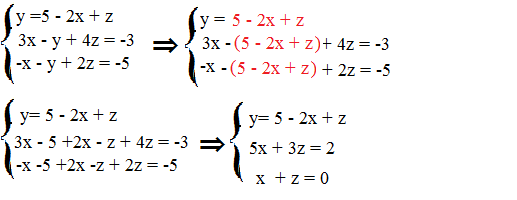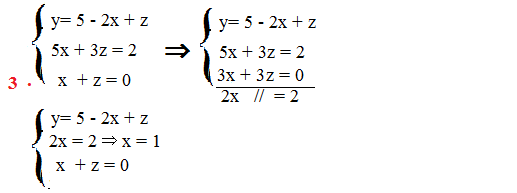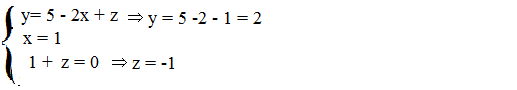Un sistema può essere costituiti da due o più equazioni e ciascuna equazione può avere più di due incognite.
Affinchè il sistema sia determinato. quindi abbia un numero finito di soluzioni, occorre che vi siano un numero di equazioni pari al numero di incognite presenti. Se il numero delle equazioni supera quello delle incognite , il sistema risulta impossibile , se il numero delle equazioni è inferiore a quello delle incognite, il sistema risulta indeterminato.
Questo tipo di sistemi si risolvono alla stessa maniera dei sistemi lineari a due incognite, quindi con il metodo della sostituzione, confronto, Cramer e riduzione.
La maggior parte delle volte per semplicità si usa il metodo della sostituzione e della riduzione.
Applichiamo prima il metodo sella sostituzione ed esplicitiamo la y nella prima equazione.
Adesso possiamo applicare il metodo della riduzione alla seconda e alla terza equazione , moltiplichiamo per 3 la terza equazione e sottraiamo membro a membro.
Nel terzo sistema come prima equazione ho riportato sempre la stessa, cioè quella con esplicitato la y, la seconda è il risultato della riduzione e la terza è la più semplice delle equazioni.
La soluzione del sistema è (1; 2; -1)
Vedi gli esercizi
Vedi programma di matematica secondo superiore